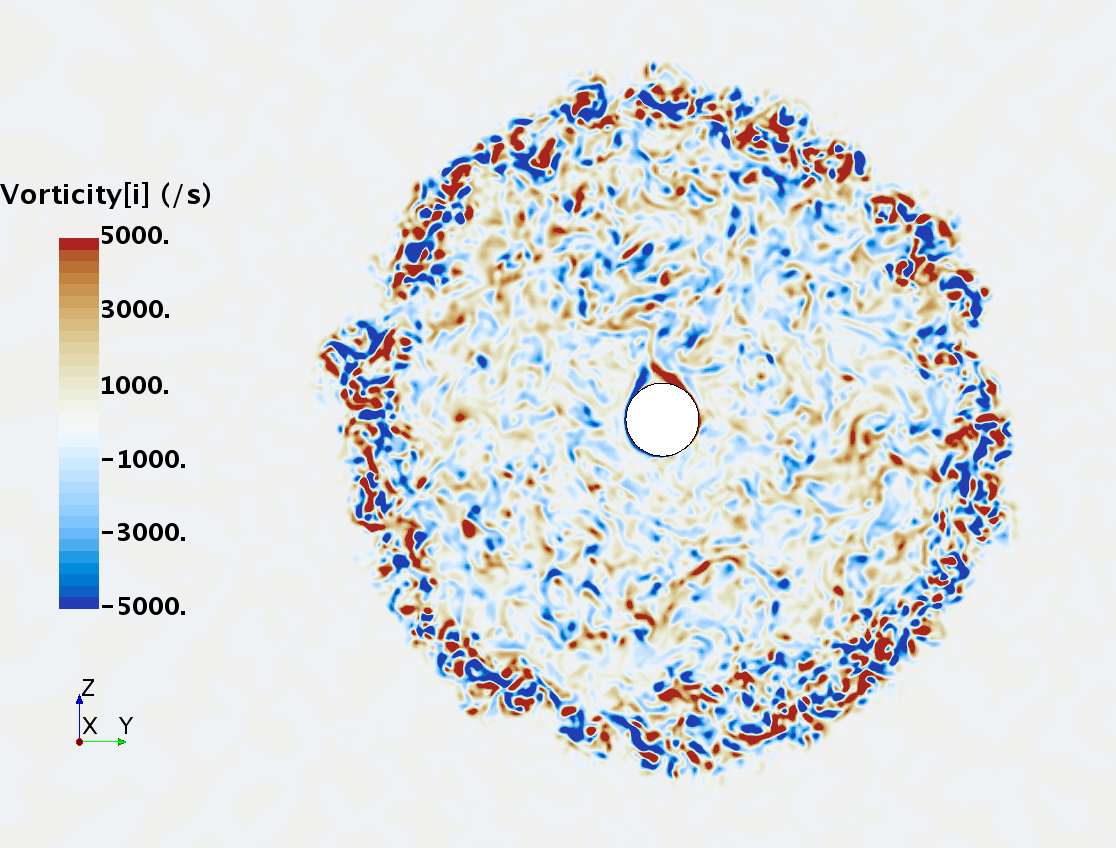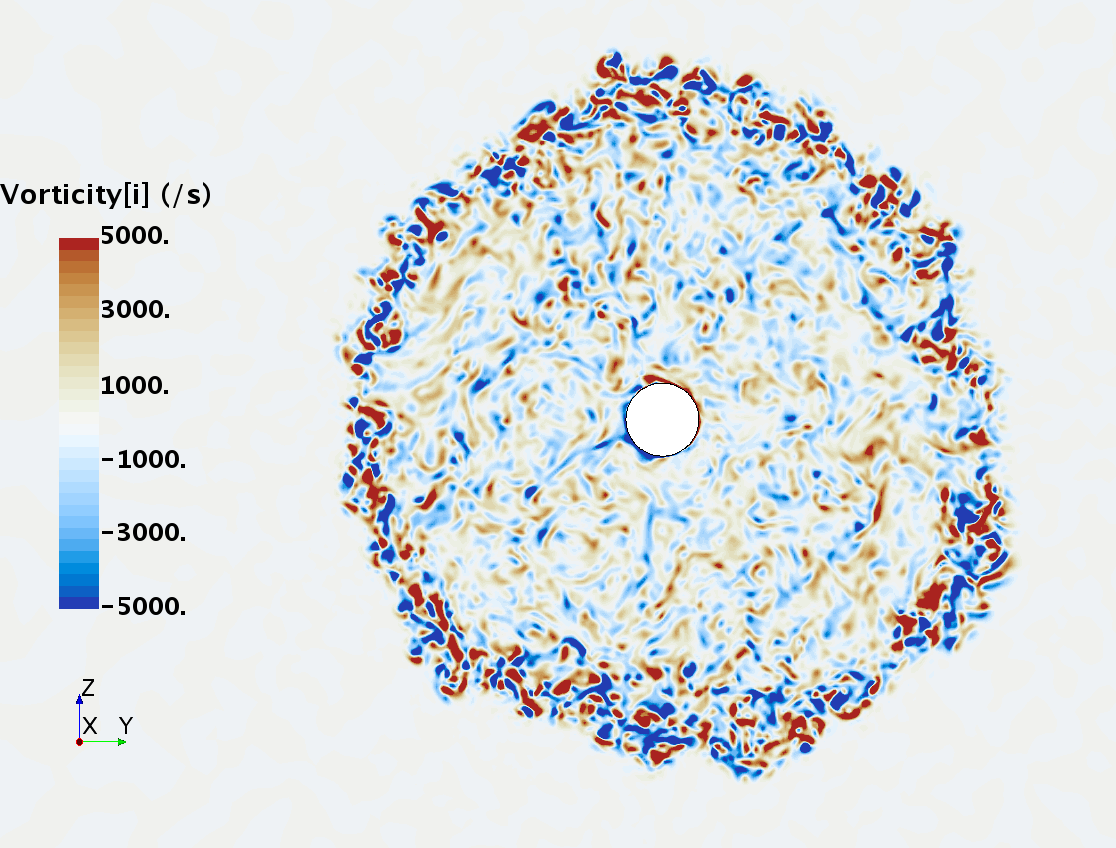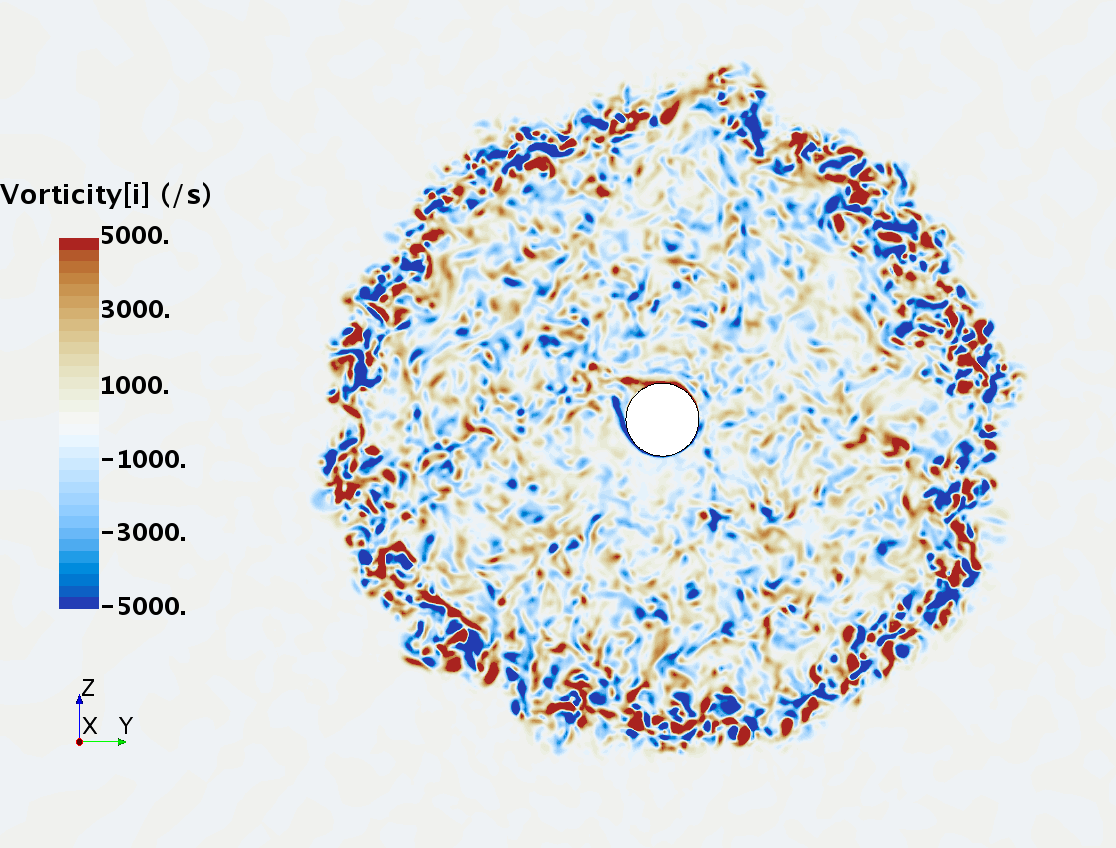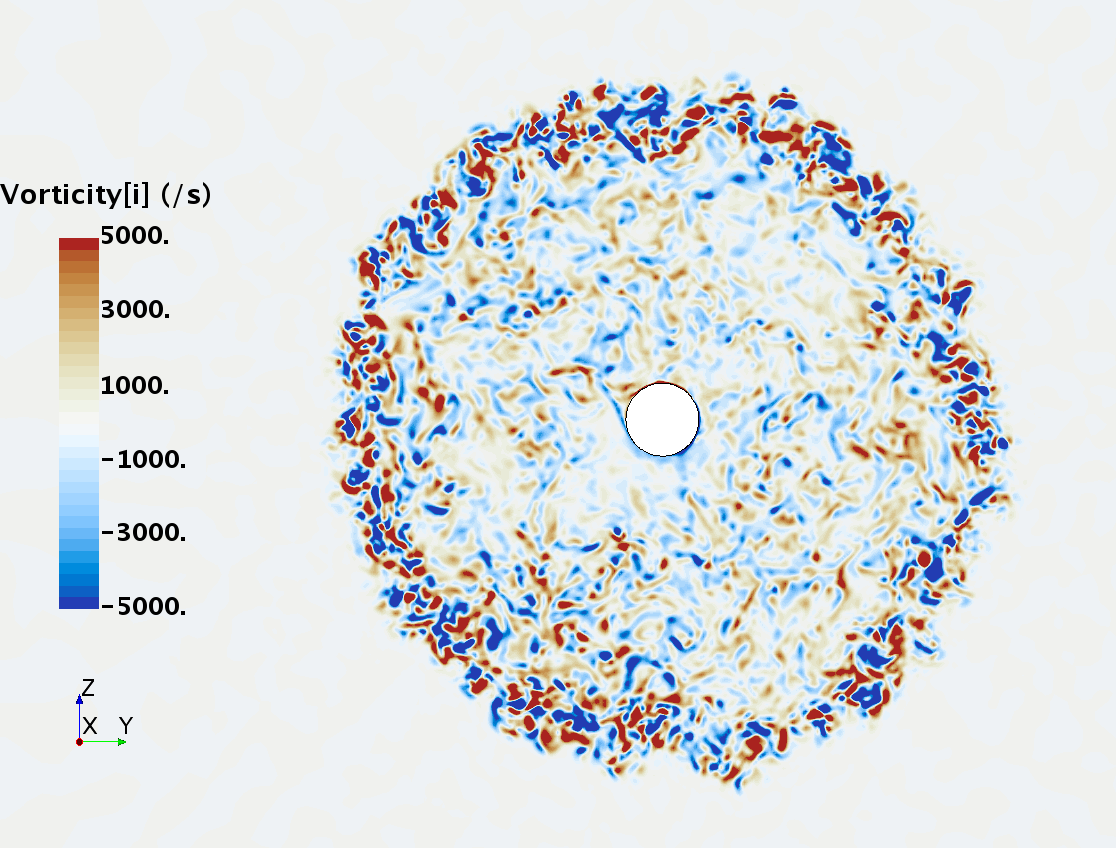Computational Methods for Fluid Dynamics

The Book

The first edition of this book was published in English in 1996; the second edition followed two years later, and the third edition appeared in 2002. Japanese version of the 3rd edition was published in 2003 and a German version in 2008. The publisher (Springer) has sold licenses for translations into Russian and Greek language.

Unfortunately, professor Joel H. Ferziger passed away on August 16, 2004. Milovan Perić moved in 2002 from university to a CFD software vendor (CD-adapco; aquired by Siemens in 2016). Both facts lead to a long pause in the work on a new edition of the book. In 2011, professor emeritus Robert L. Street from Stanford University joined Milovan Perić and the work on the 4th edition started. For various reasons this work slowed down for a while, but was intensified in 2017 and 2018, leading to the release of the 4th edition in summer 2019. Kerstin and Milovan Perić worked hard on the translation into German and so the 2nd German edition appeared in 2020.

The 4th edition represents a substantial re-writing, especially of Chapters 7 and 8 which deal with methods for solving the Navier-Stokes equations. While previous editions were heavily focused on SIMPLE-type methods, now the Fractional Step Methods receive an equal attention. Some versions that were not published before are included; they have proven to be competitive to - and maybe even more attractive than - SIMPLE-type algorithms. There is also more information on discretization methods using arbitrary polyhedral grids and overlapping grids. Chapter on simulation of turbulent flows has also be completely re-written and other Chapters also contain major extensions.

The set of computers codes for solving linear equation systems and for solving the Navier-Stokes equations on Cartesian and non-orthogonal grids using 2nd-order discretization and SIMPLE-algorithm will soon be extended to include the versions based on Fractional Step Methods. Additional notes on various aspects of CFD that could not be included in the book will also appear in the Download Center.

In May 2024, Milovan started with preparation of book-based lecture notes for teaching CFD. The project is sponsored by Siemens and involves videos of lectures in English published on YouTube-channel "@MilovanPericCFD", PowerPoint-files of lecture notes in English, source code of simple programs demonstrating features of numerical methods, and simulation files for test cases computed with Simcenter STAR-CCM+ software (all downloadable from a Siemens community website Peric Lectures on CFD).

The lectures include many details and examples which are not available in the book, especially on testing the order of various approximations, and on application of finite-difference (FD) and finite-volume (FV) methods to various test cases. In addition to sample codes available here in the Download Center, new codes were written to demonstrate the performance of FD and FV methods of 1st, 2nd and 4th order in one- and two-dimensional problems. These codes are available in FORTRAN, Python, and C++ languages at the above Siemens community site. Codes for solving the Navier-Stokes equations in two dimensions will also be available in both SIMPLE and Fractional Step Method versions. More advises for practical applications of CFD are also included in those lectures.

The current project "CFD I" handles the topics covered by book Chapters 1 to 8; another set "CFD II" is planned to follow, covering the remaining 5 chapters. The lectures are being published as they are finished; at the time of writing this text, 10 lectures were online.

The lectures are intended for both engineering students at universities and engineers from industry who want to learn more about CFD, and for teachers who want to teach CFD classes at their university. Teachers can translate PowerPoint presentations into their language (if different from English) and modify them to adapt to their focus of study. They can also use only certain parts of the presentation to extend their own course material. It would be nice if the book and the original lectures notes were mentioned as the source of information...

Stay tuned for more updates of this website in the near future!

News

Gallery

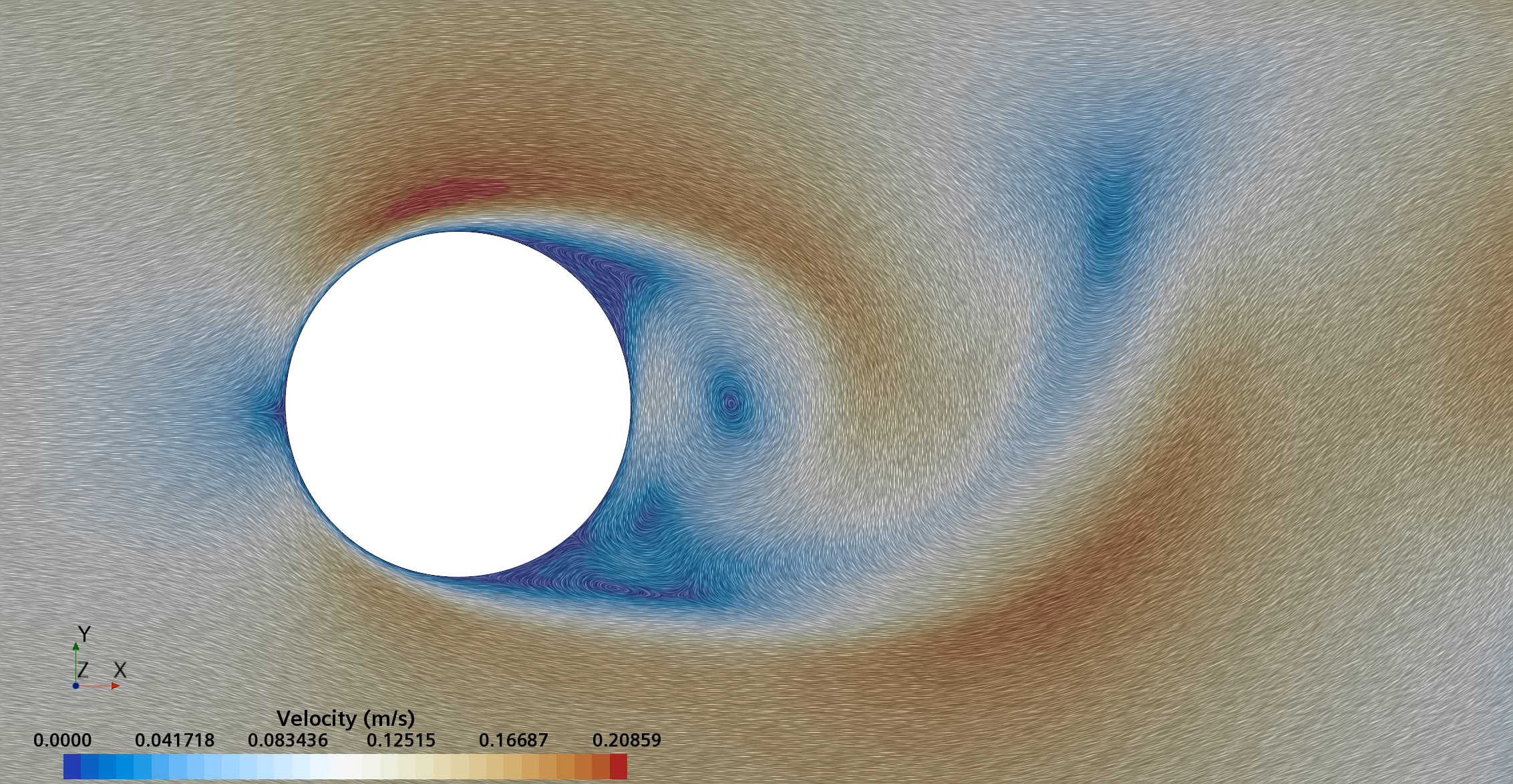
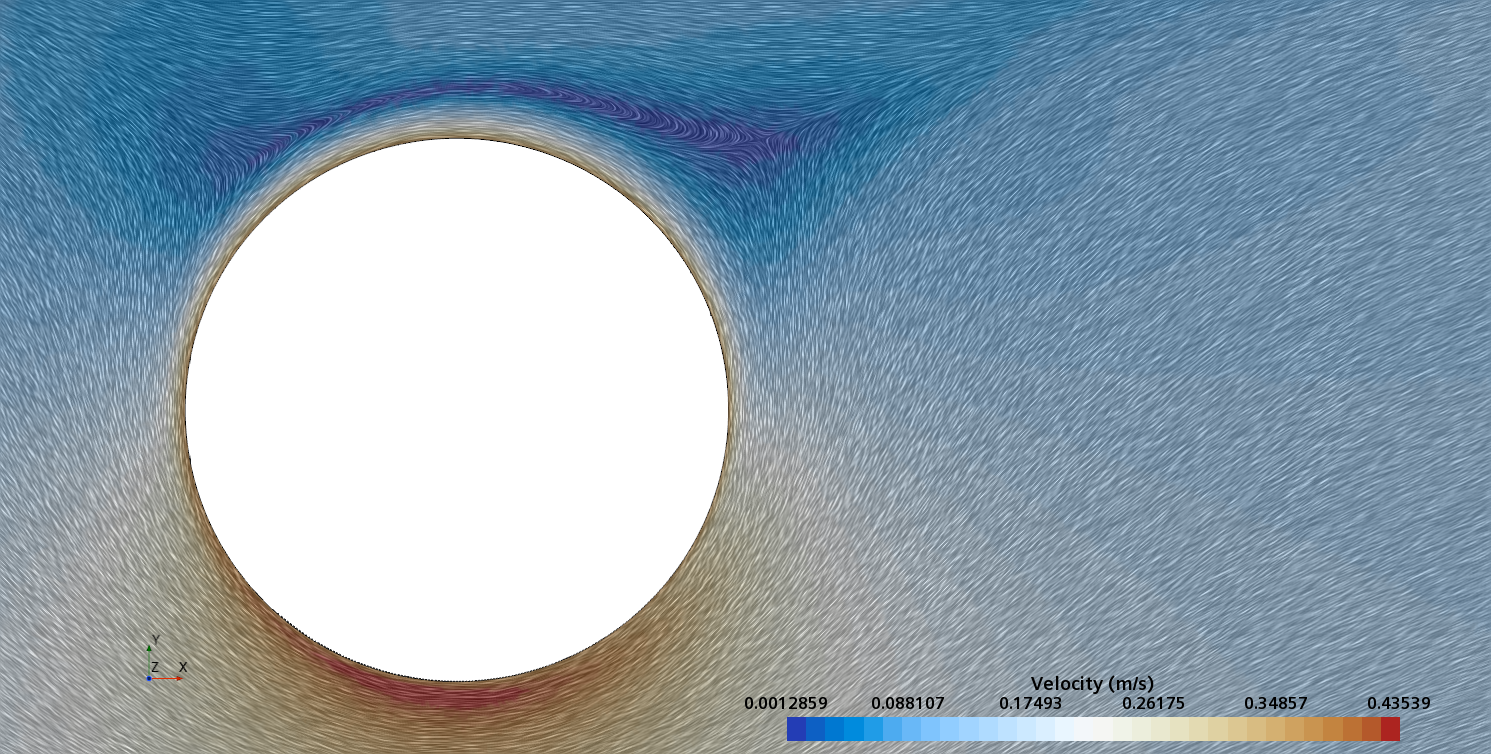
Instantaneous pattern of laminar flow around circular cylinder in an infinite environment at Re = 500: fixed cylinder (upper) and rotating cylinder (lower).

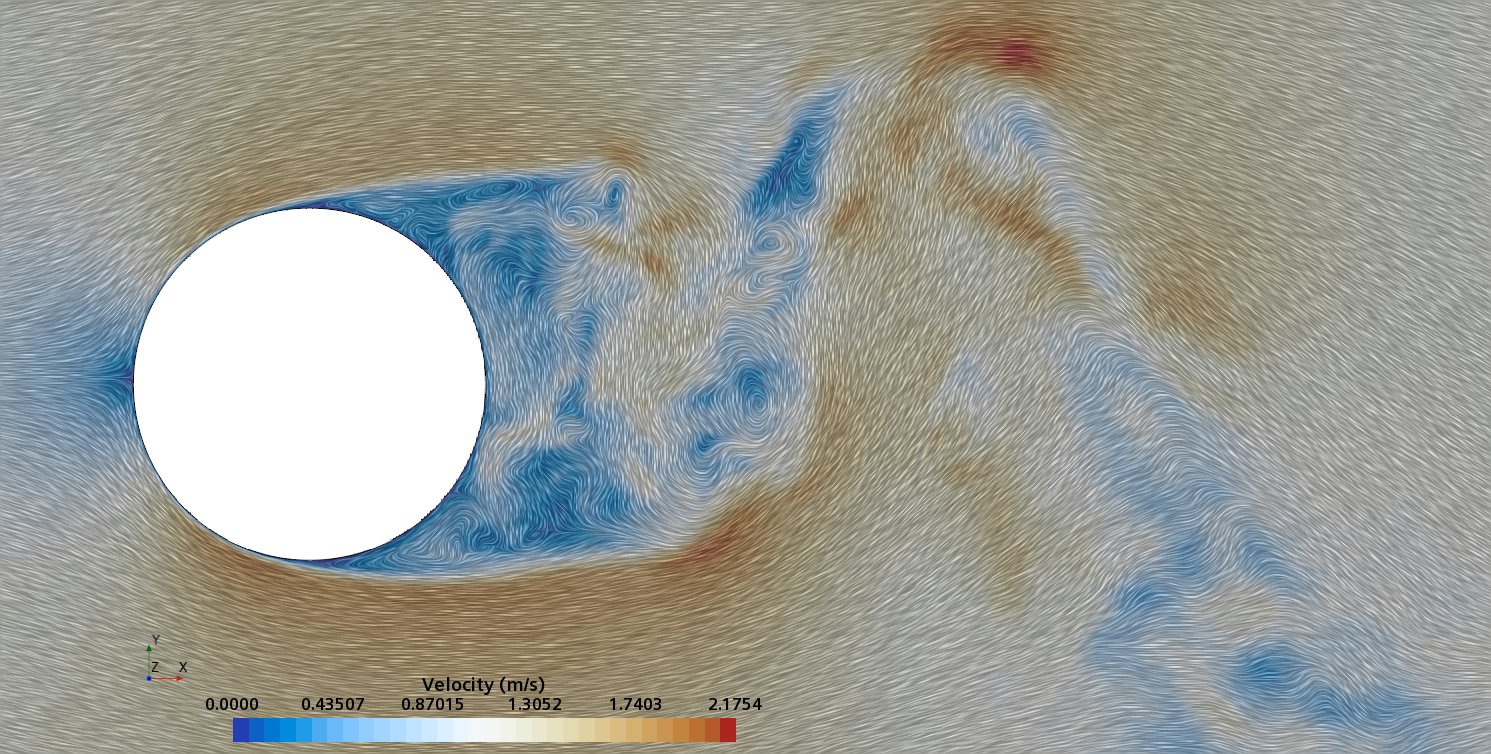
Instantaneous pattern of turbulent flow around circular cylinder in an infinite environment at Re = 5,000 (DNS).

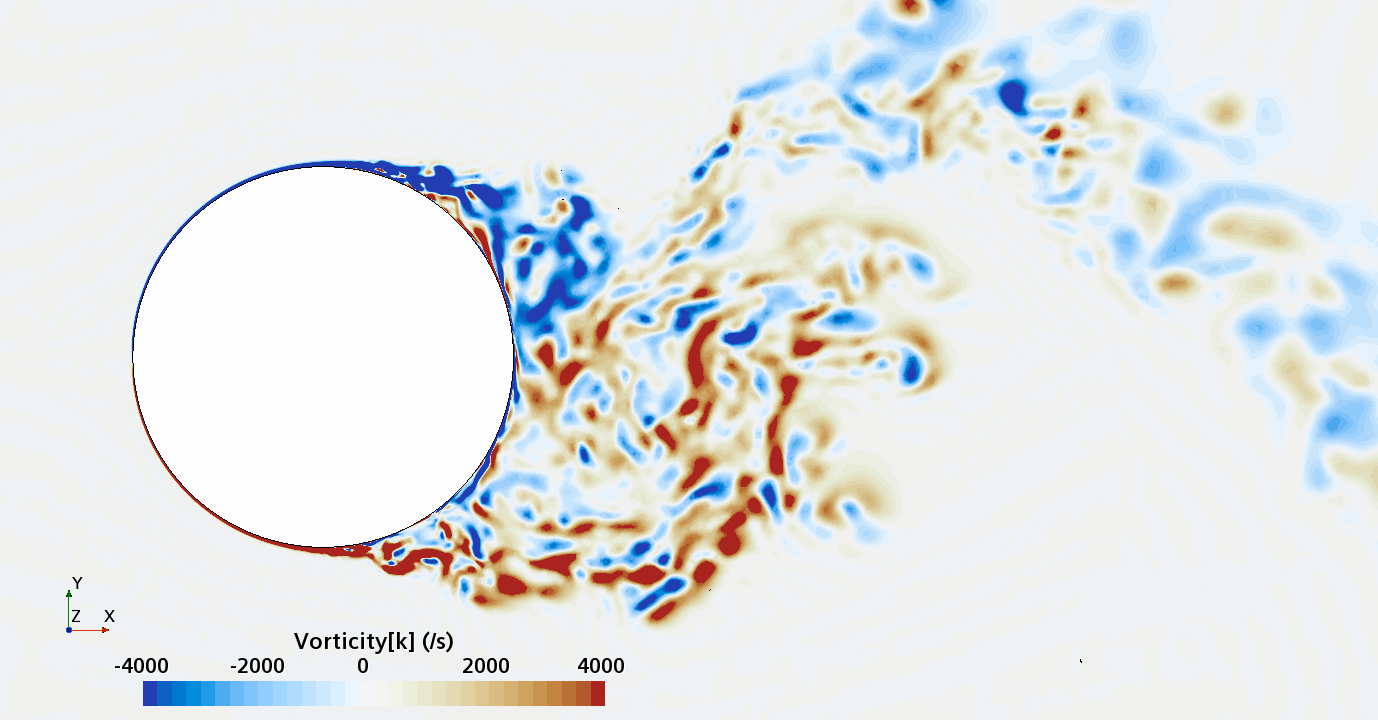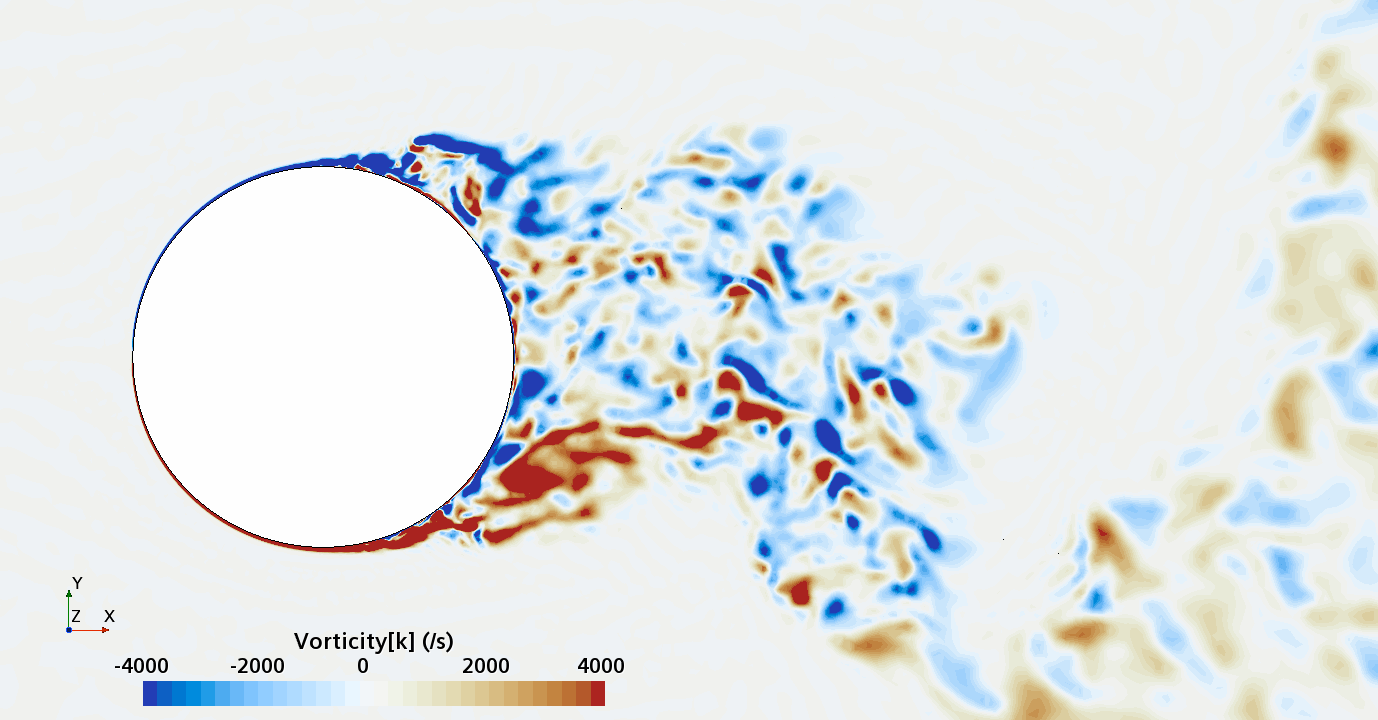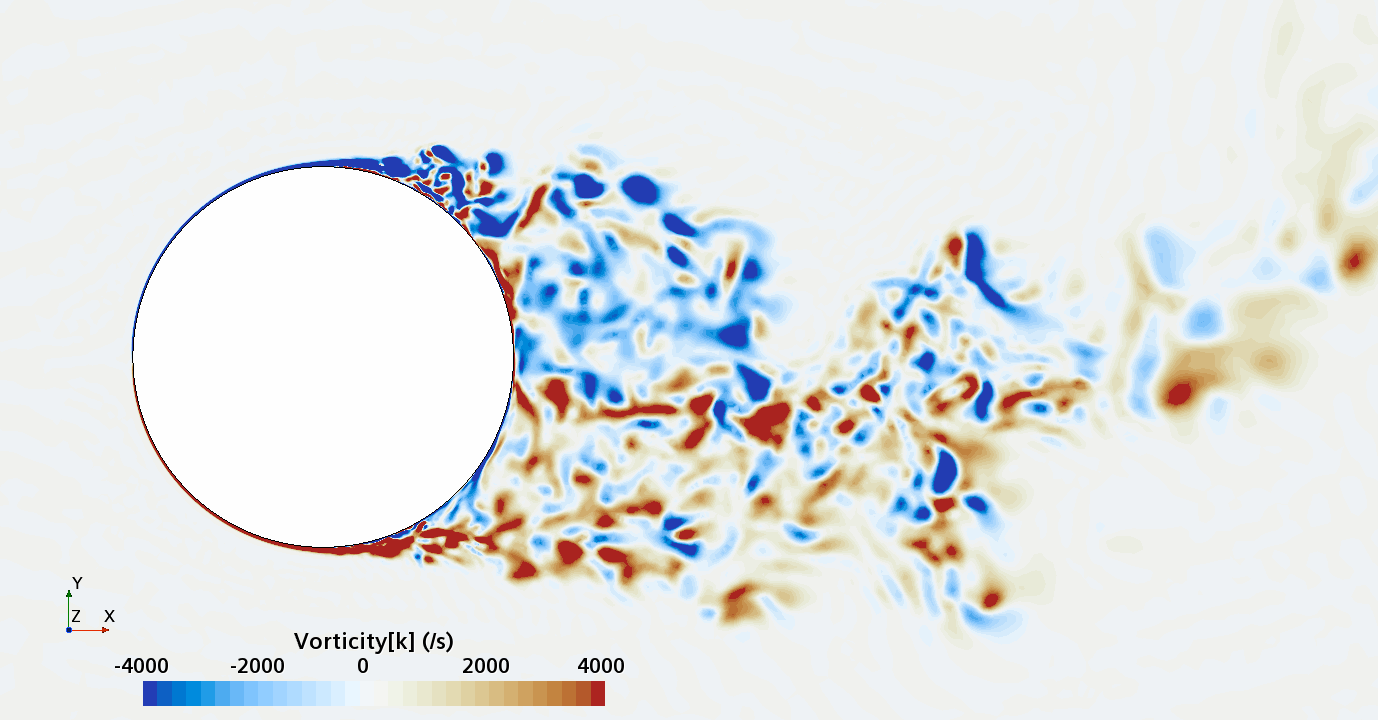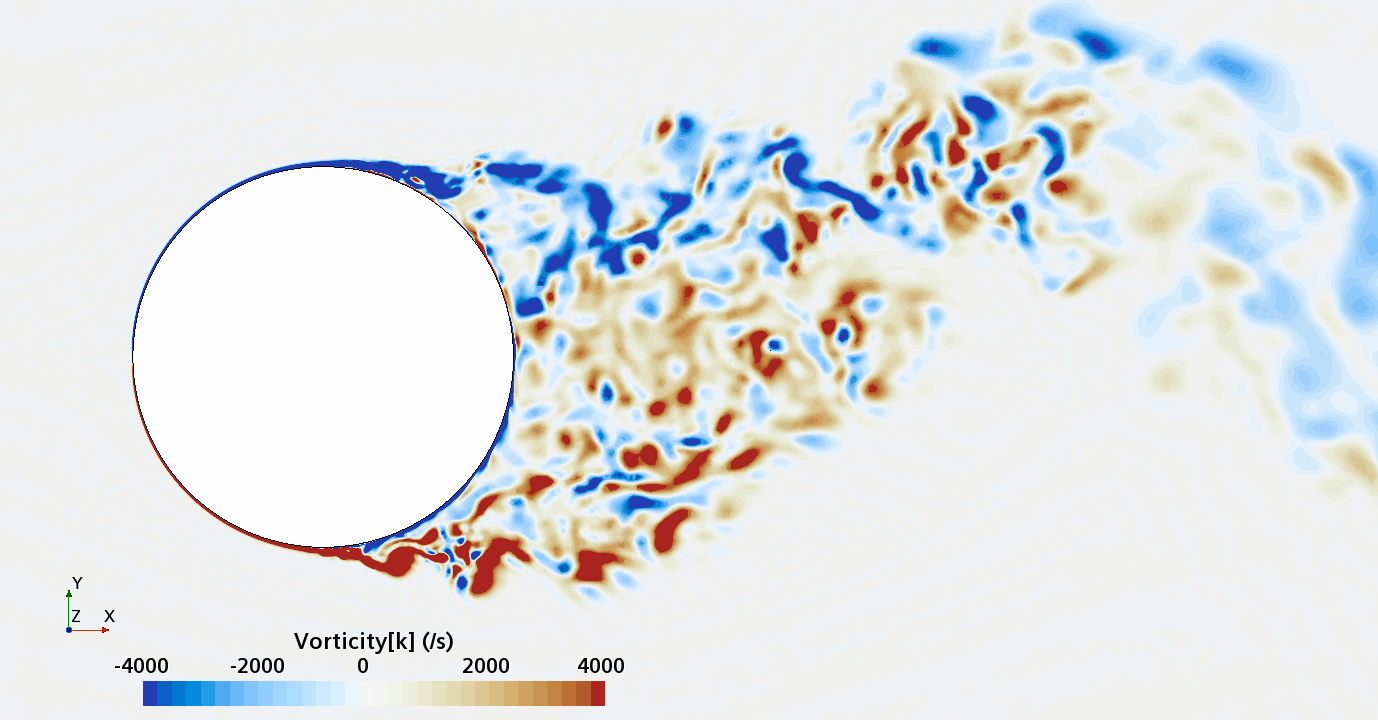
Instantaneous pattern of turbulent flow around circular cylinder in an infinite environment at Re = 50,000 (LES): Section through the grid with vorticity contours (upper) and animation of vorticity variation (lower).

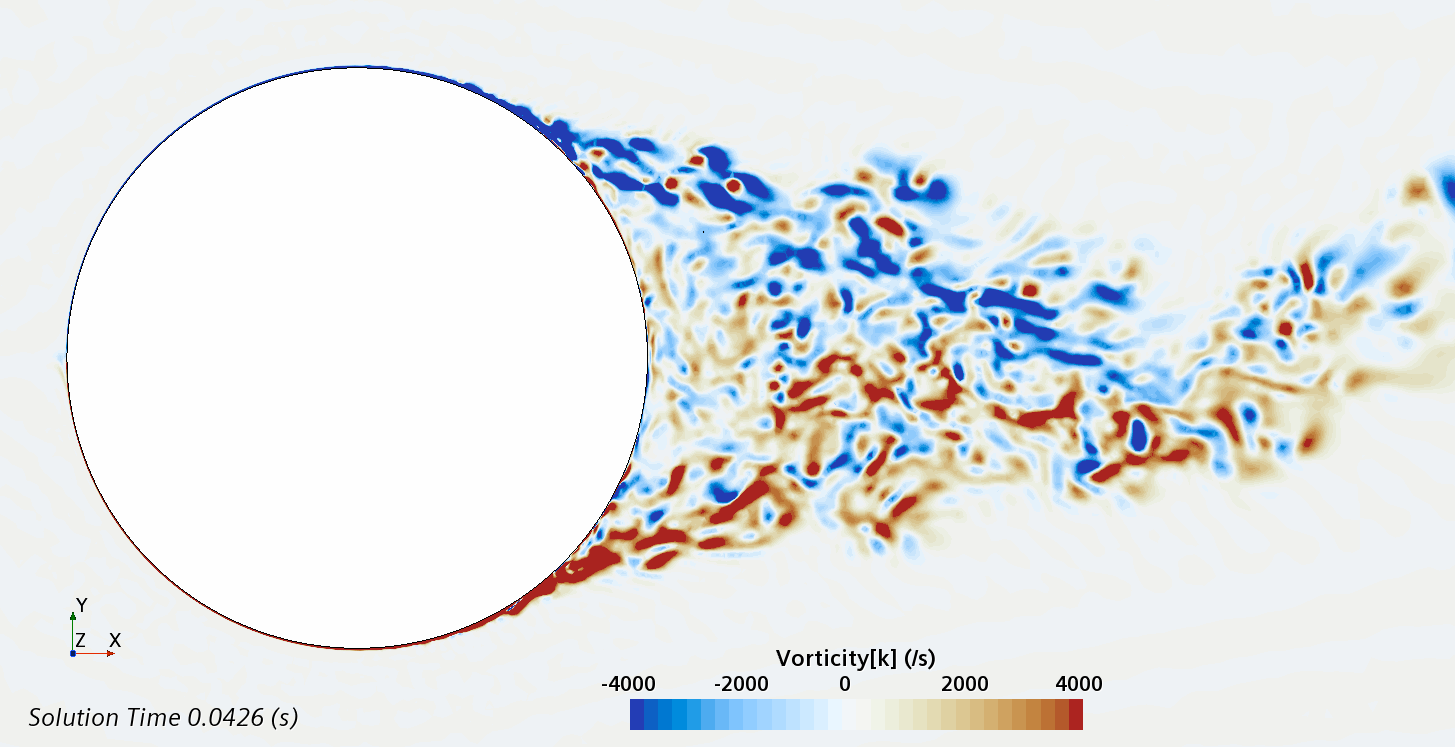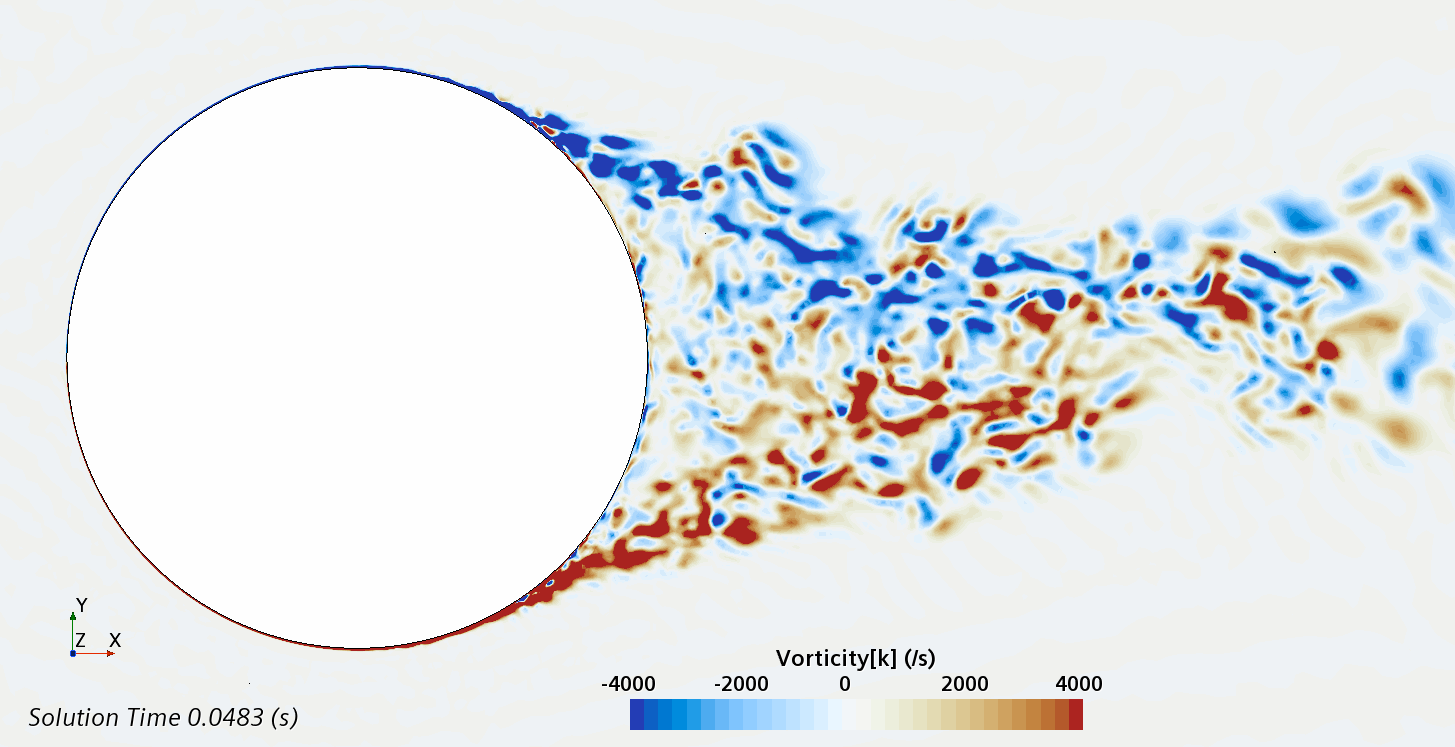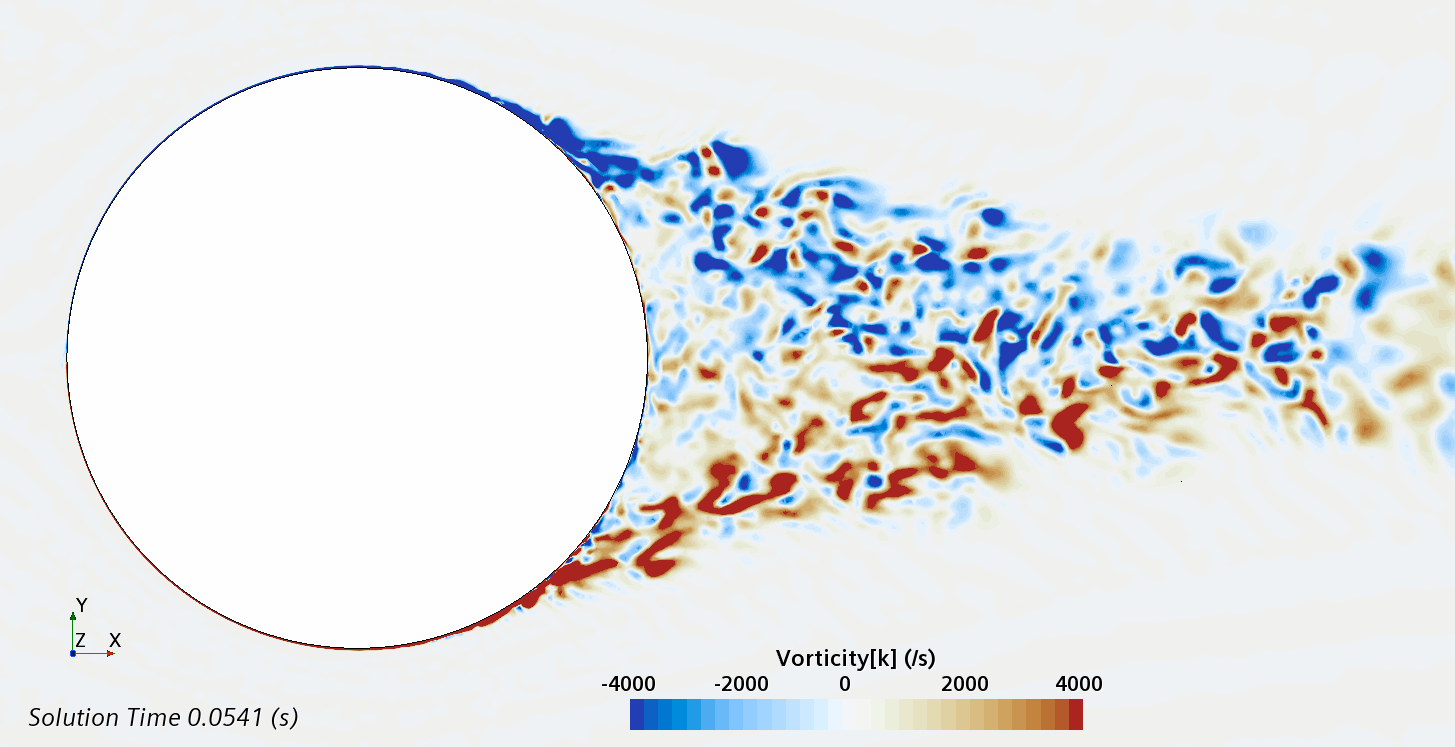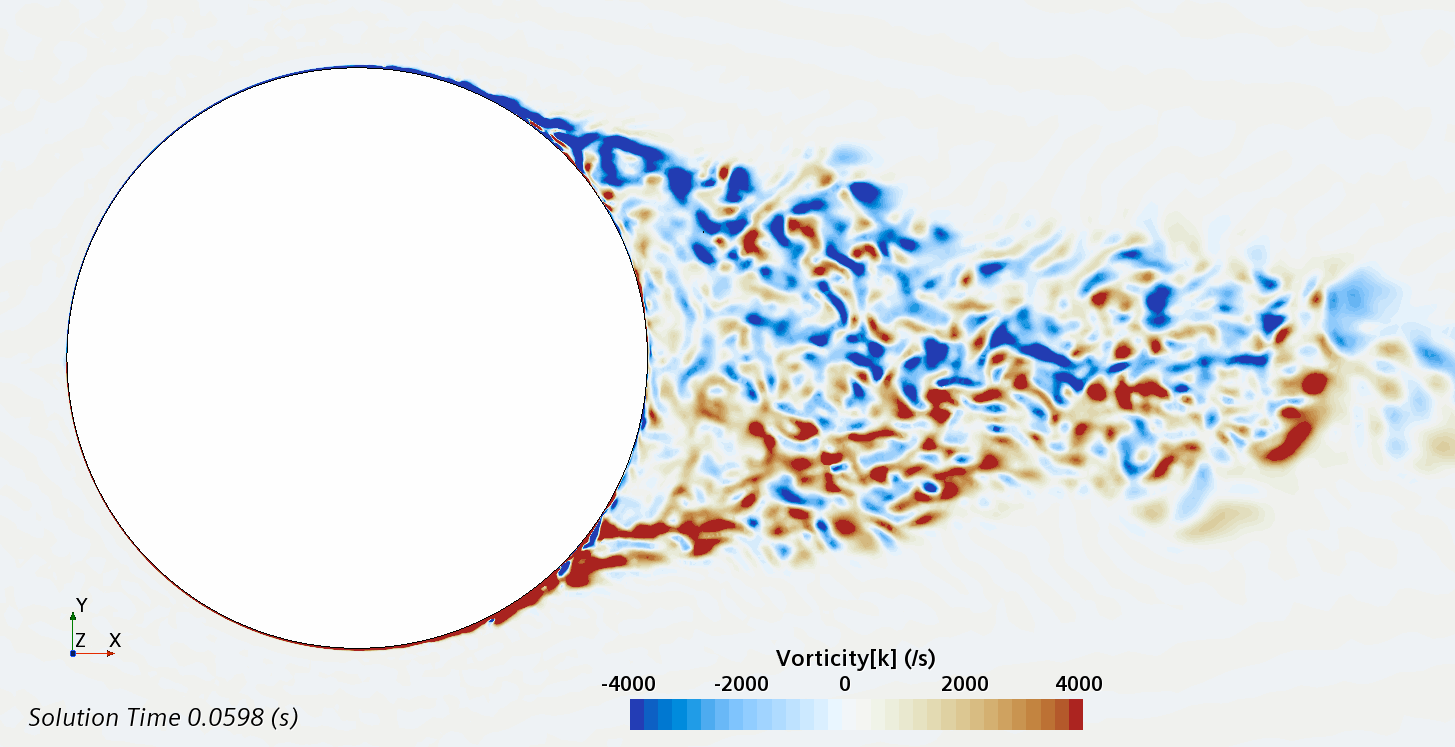
Instantaneous pattern of turbulent flow around circular cylinder in an infinite environment at Re = 500,000 (LES): animation of vorticity variation.

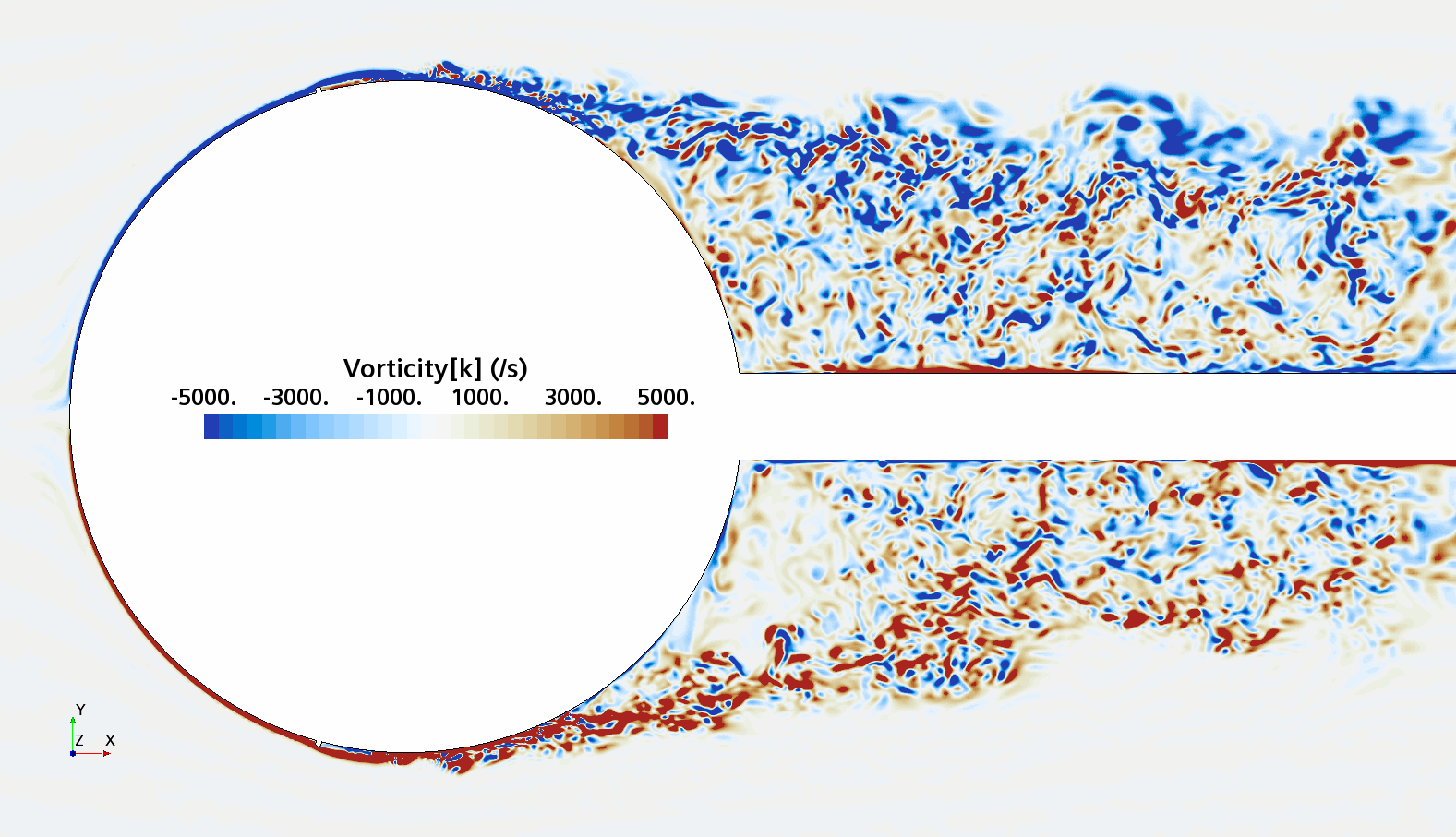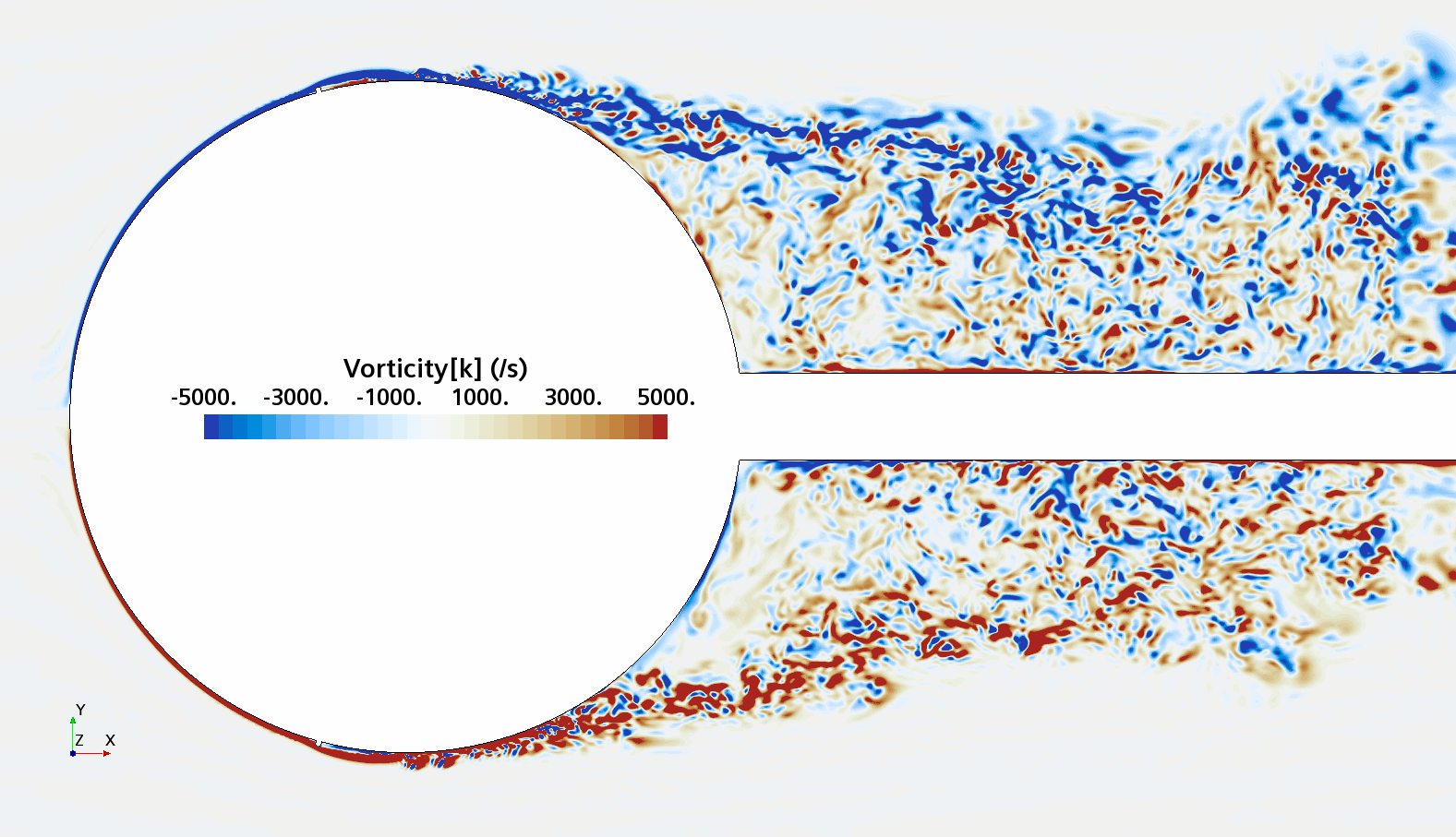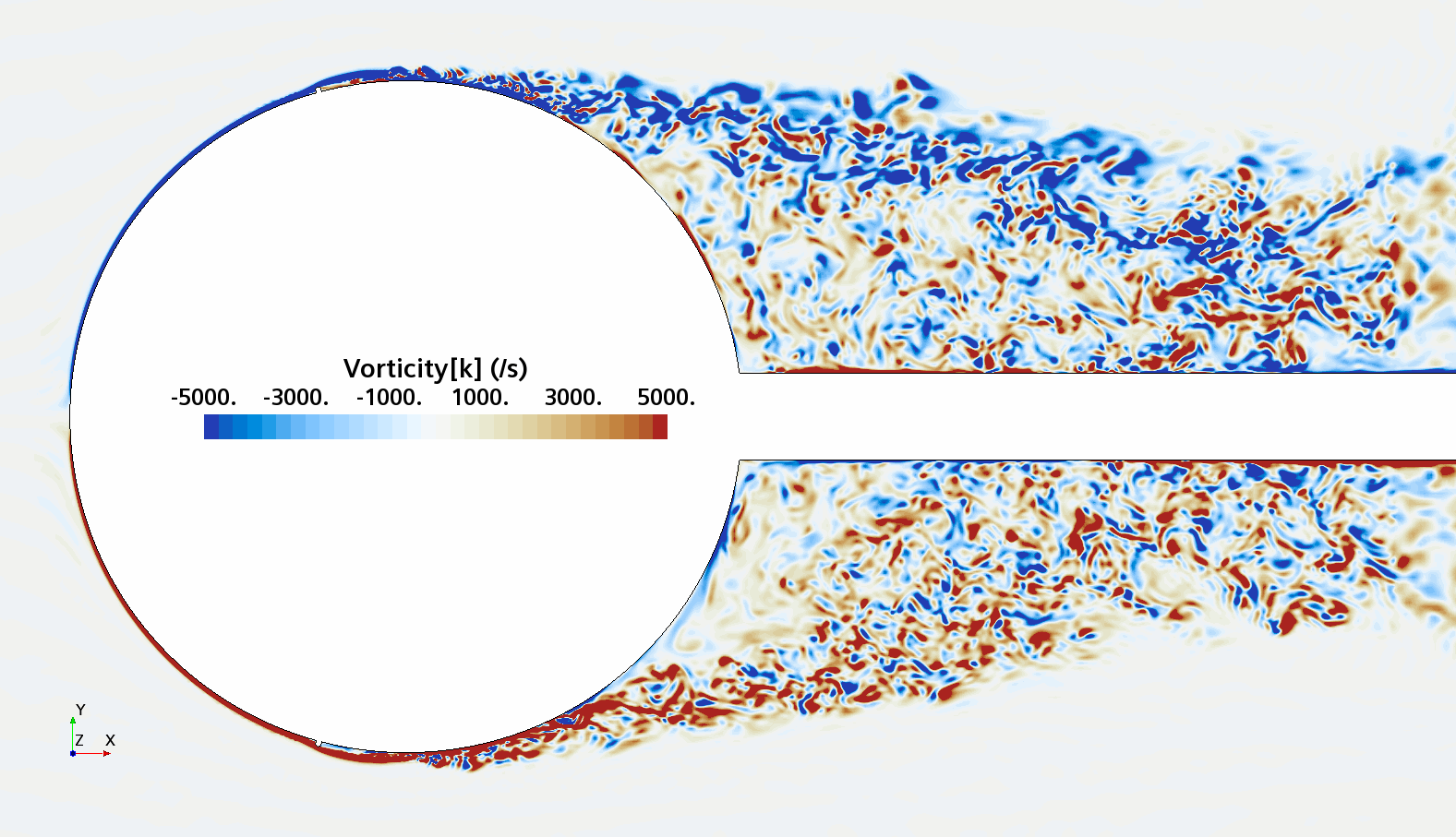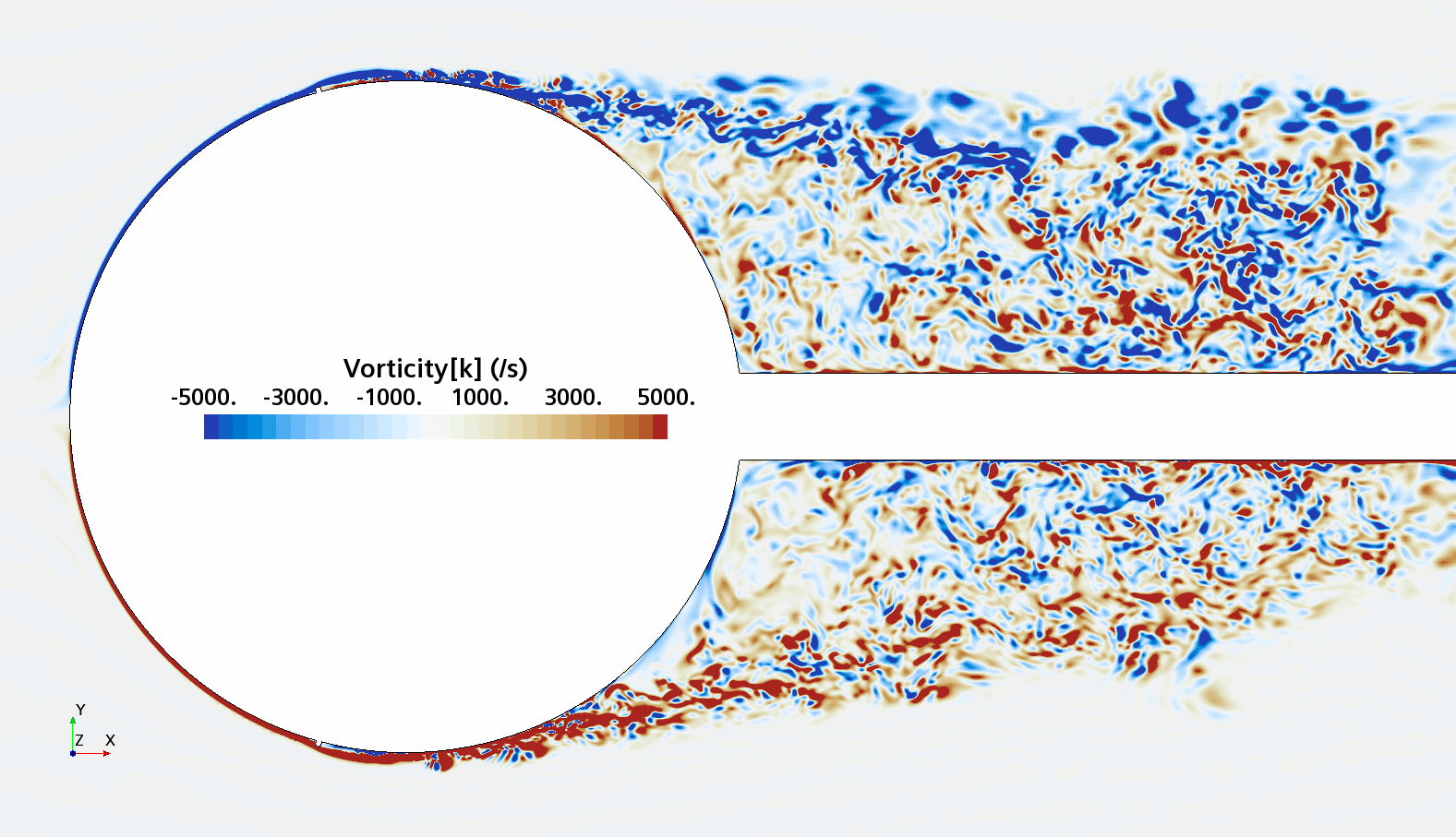
Instantaneous pattern of turbulent flow around a sphere held by a rear stick at Re = 50,000 (LES): animation of vorticity variation for a smooth sphere (upper) and a sphere with a trip wire (lower). Trip wire introduces local laminar flow separation with turbulent reattachment; the downstream turbulent boundary layer separates much later than in the case of a smooth sphere, leading to a 3 times lower drag!

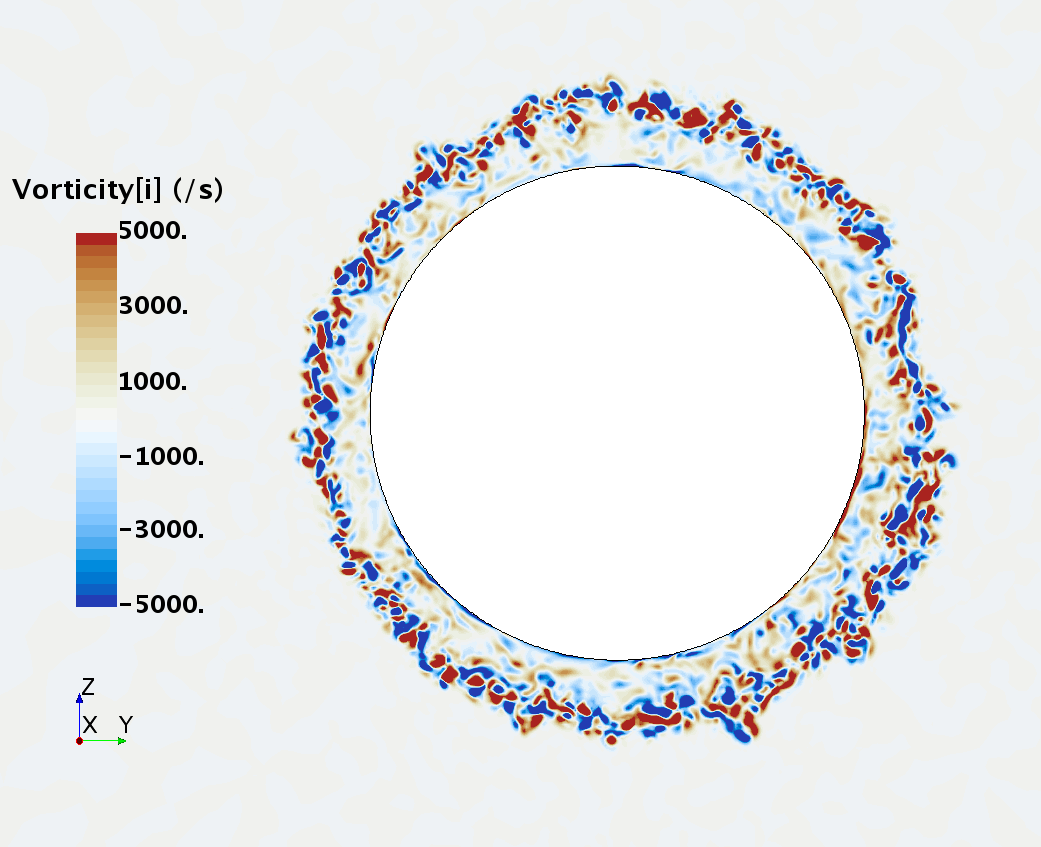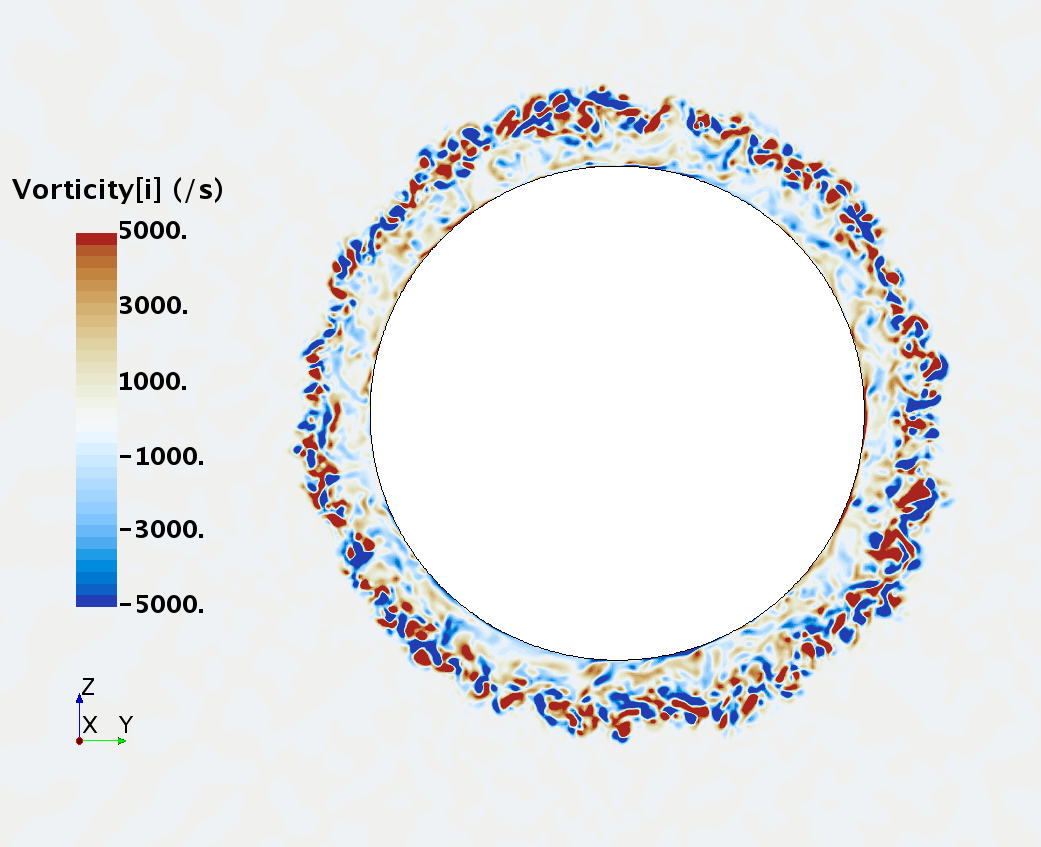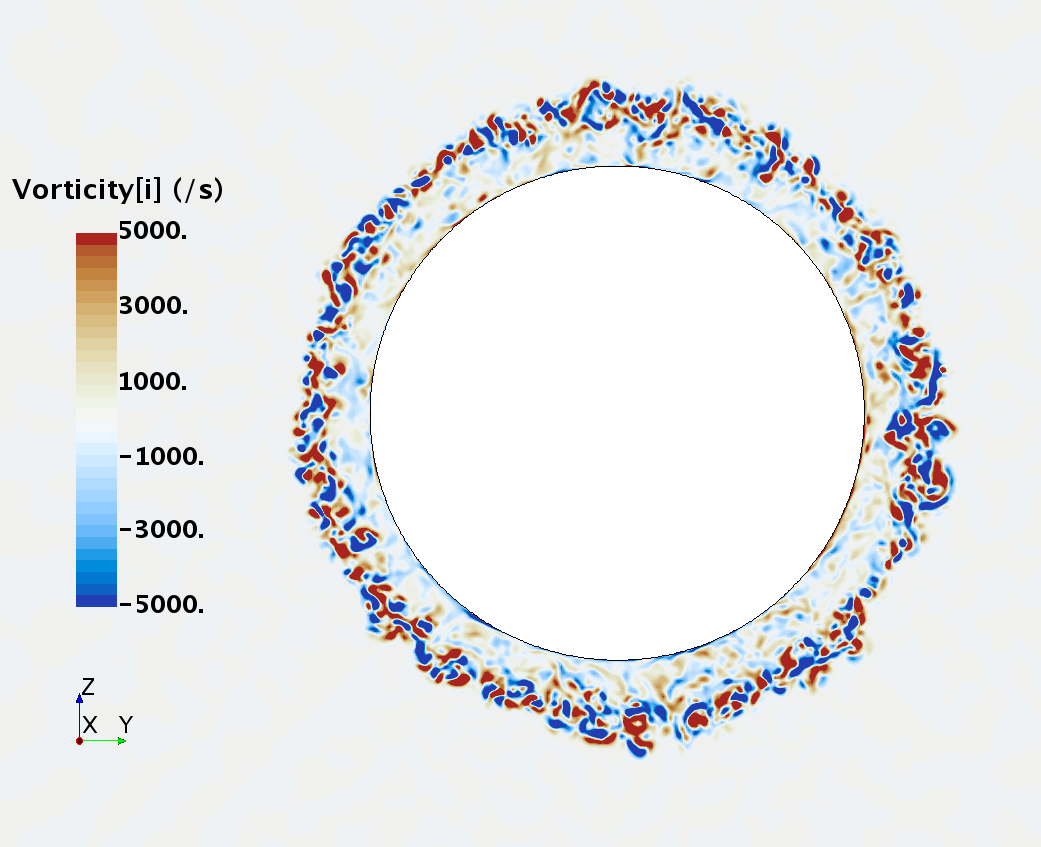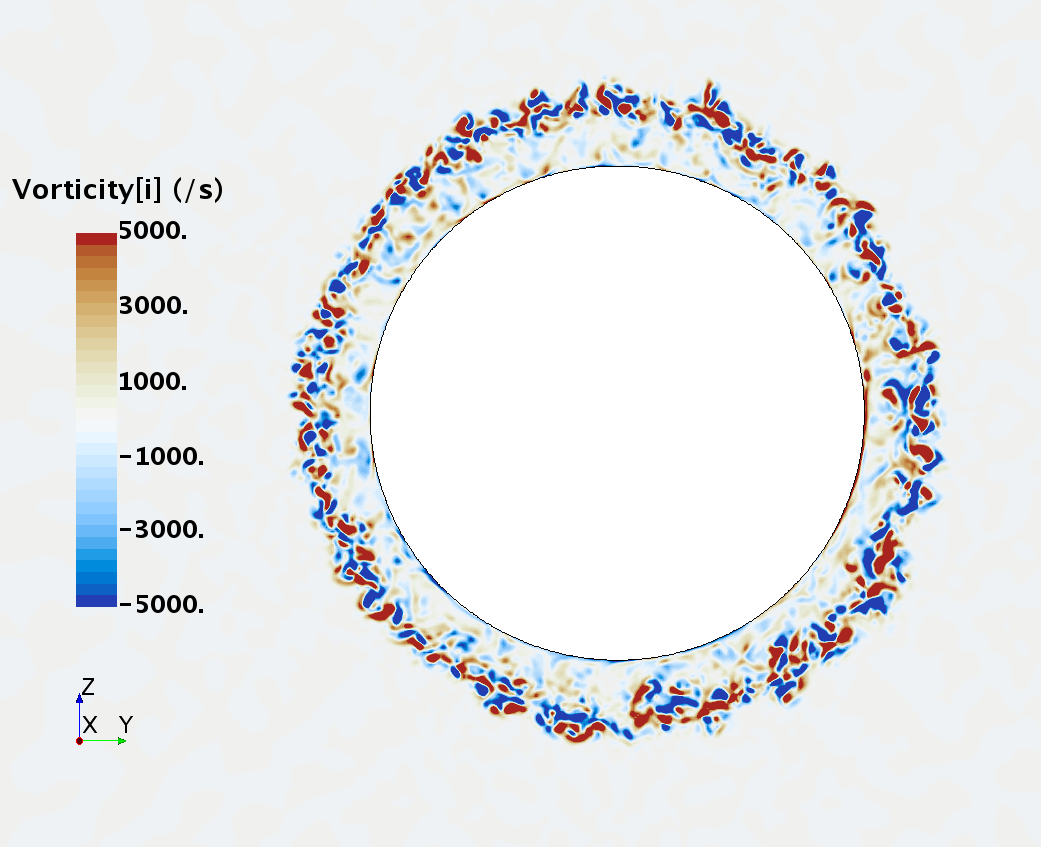
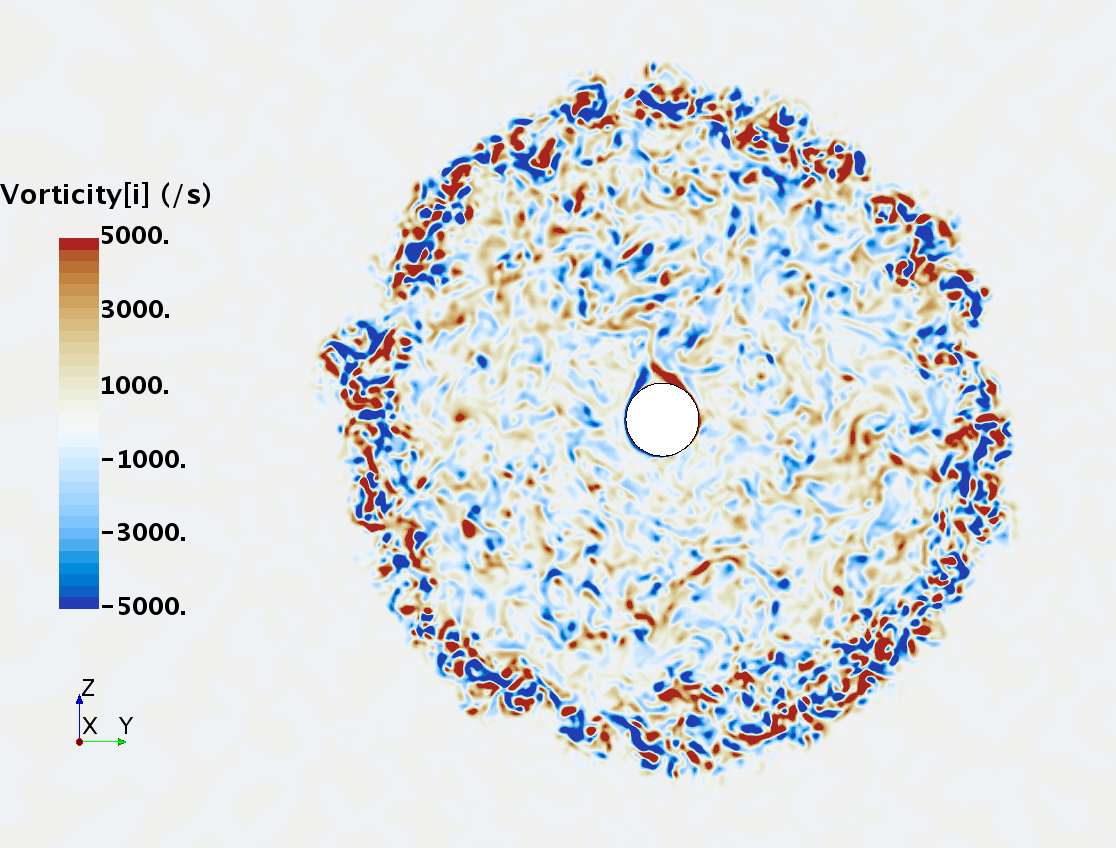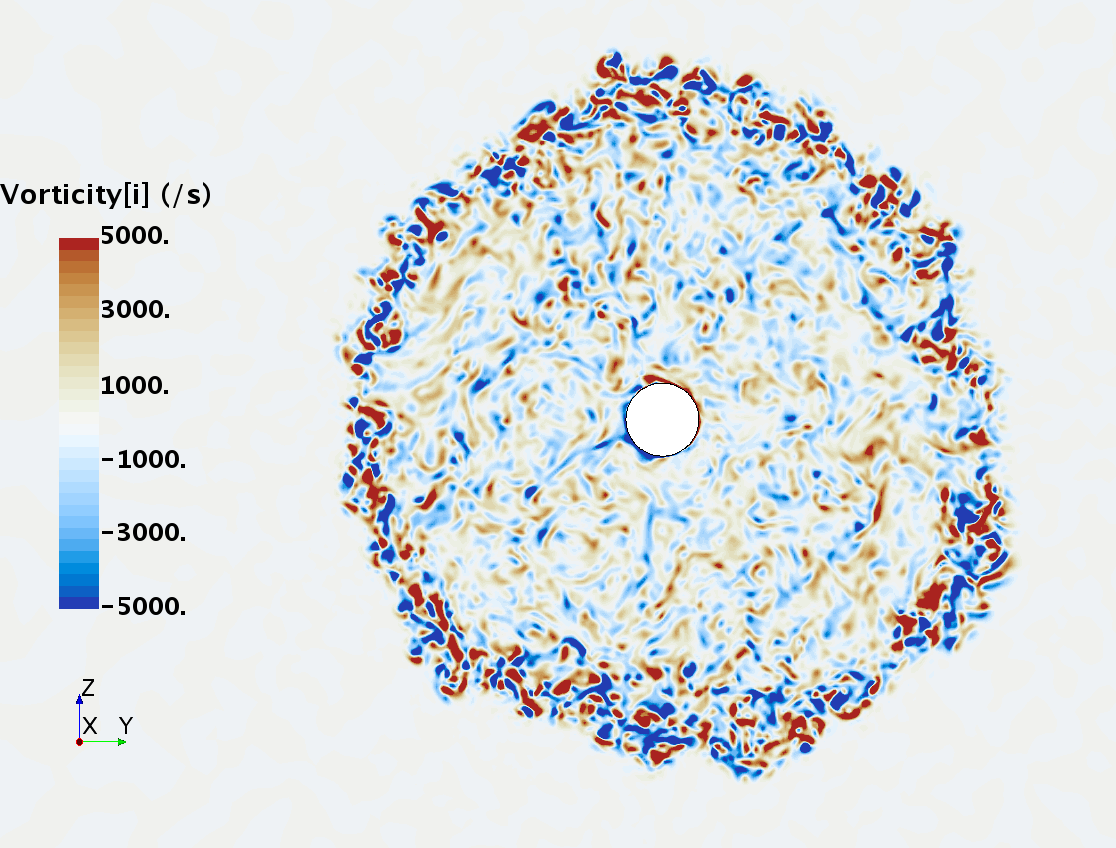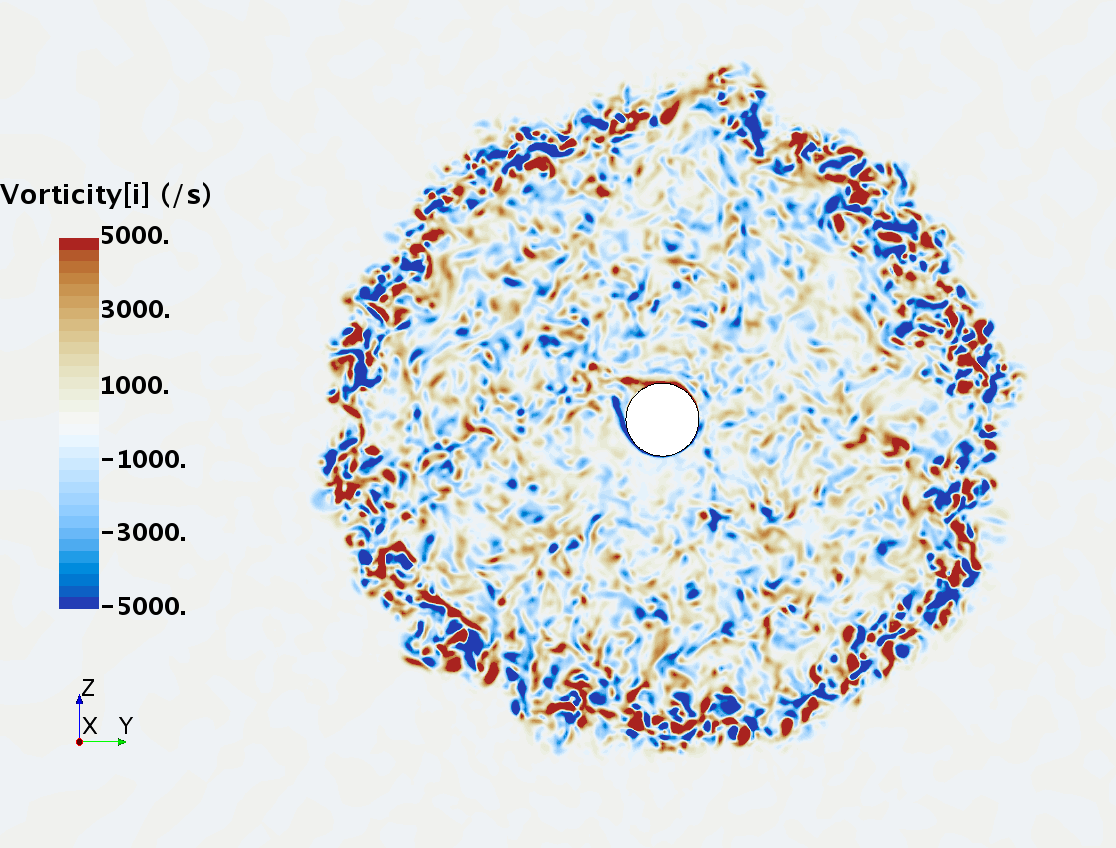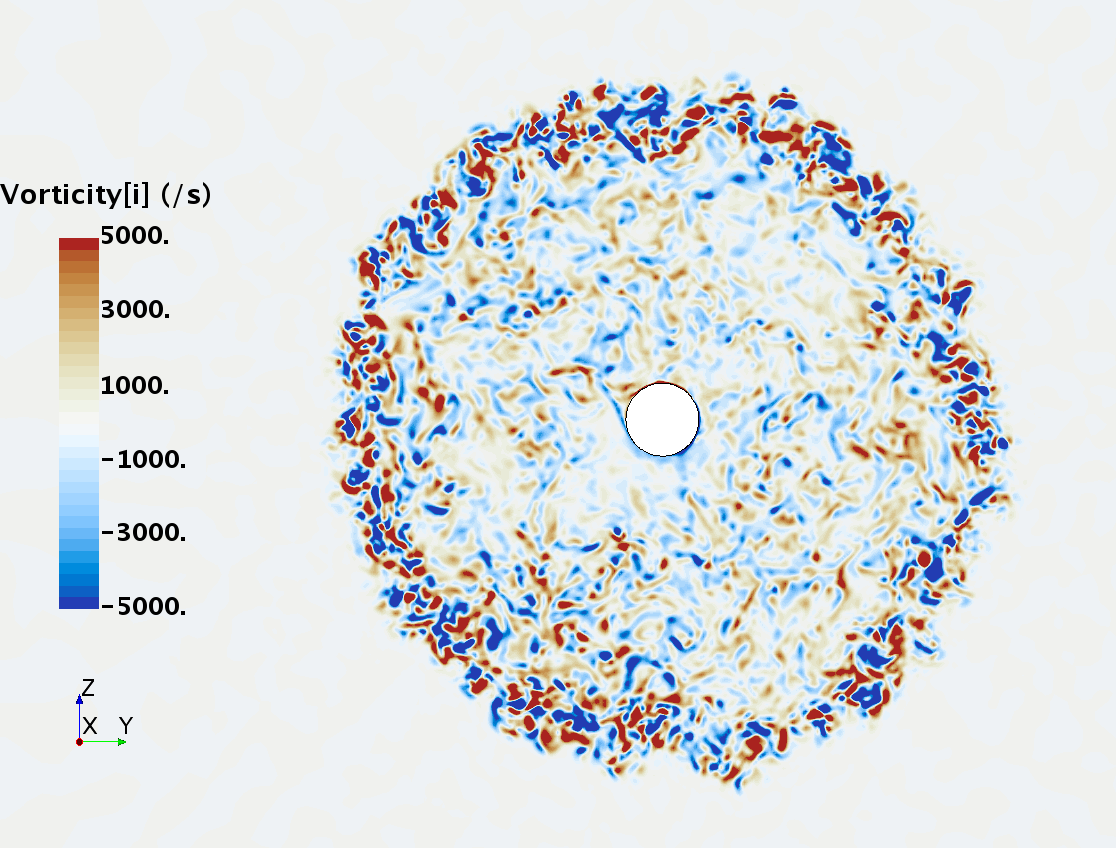
Instantaneous pattern of turbulent flow around a sphere held by a rear stick at Re = 50,000 (LES): animation of vorticity variation for a smooth sphere in cross-section at 1/4 of diameter, 1/2 diameter, 1 diameter and 1.5 diameter downstream of sphere center, respectively, from top to bottom. The top two animations show a higher intensity of turbulence at the outer edge of the separation zone (highest shear) and lower intensity within separation zone. One diameter downstream of sphere center the whole wake is strongly turbulent but still relatively centered around the stick, while 1.5 diameters downstream of sphere center the wake is meandering around the stick and some zones are only intermittently turbulent.

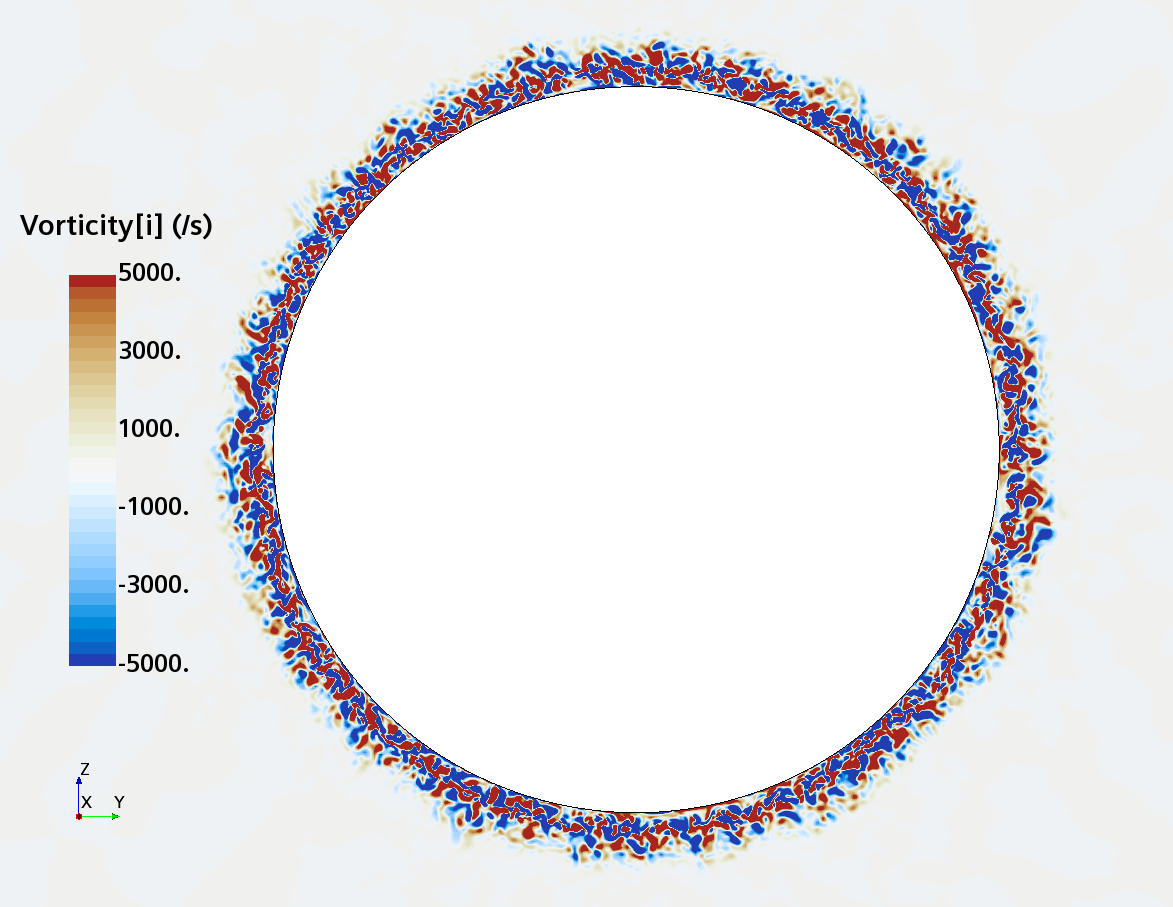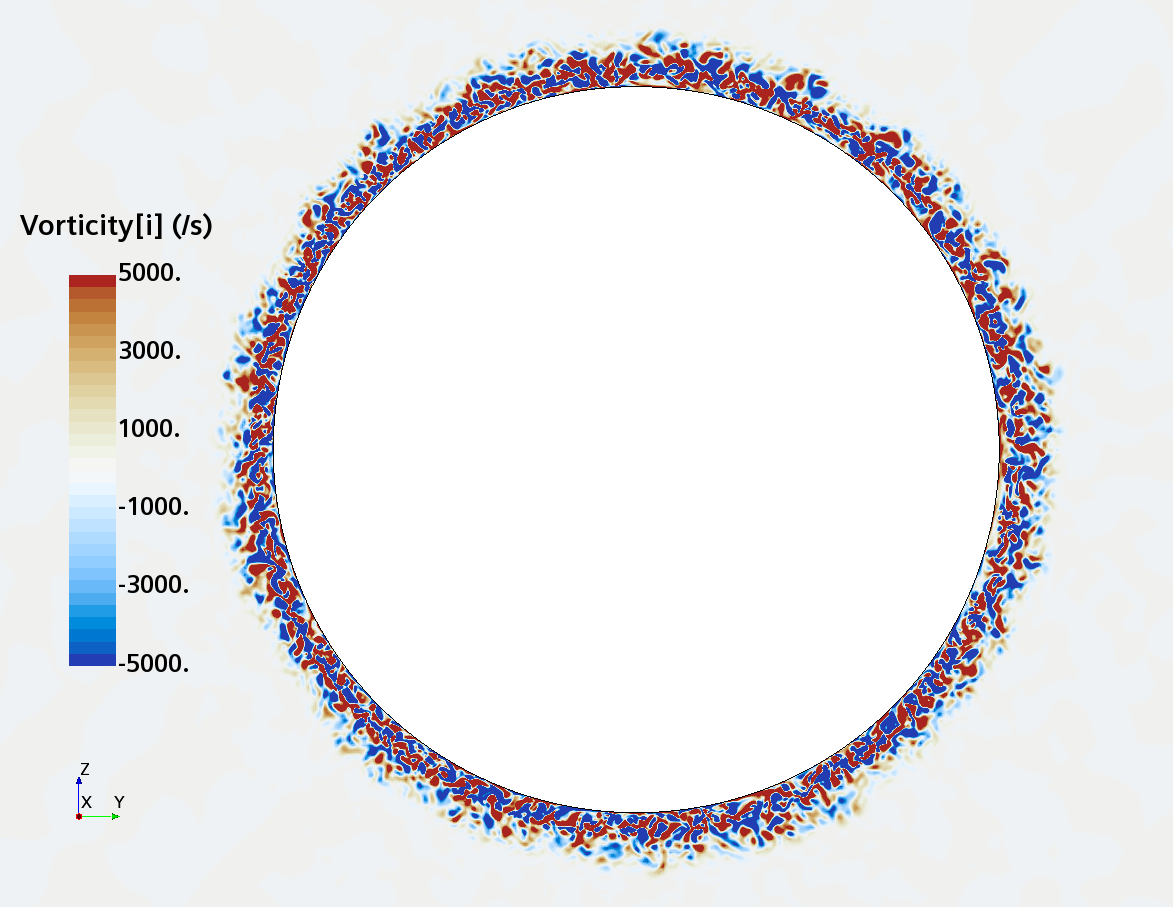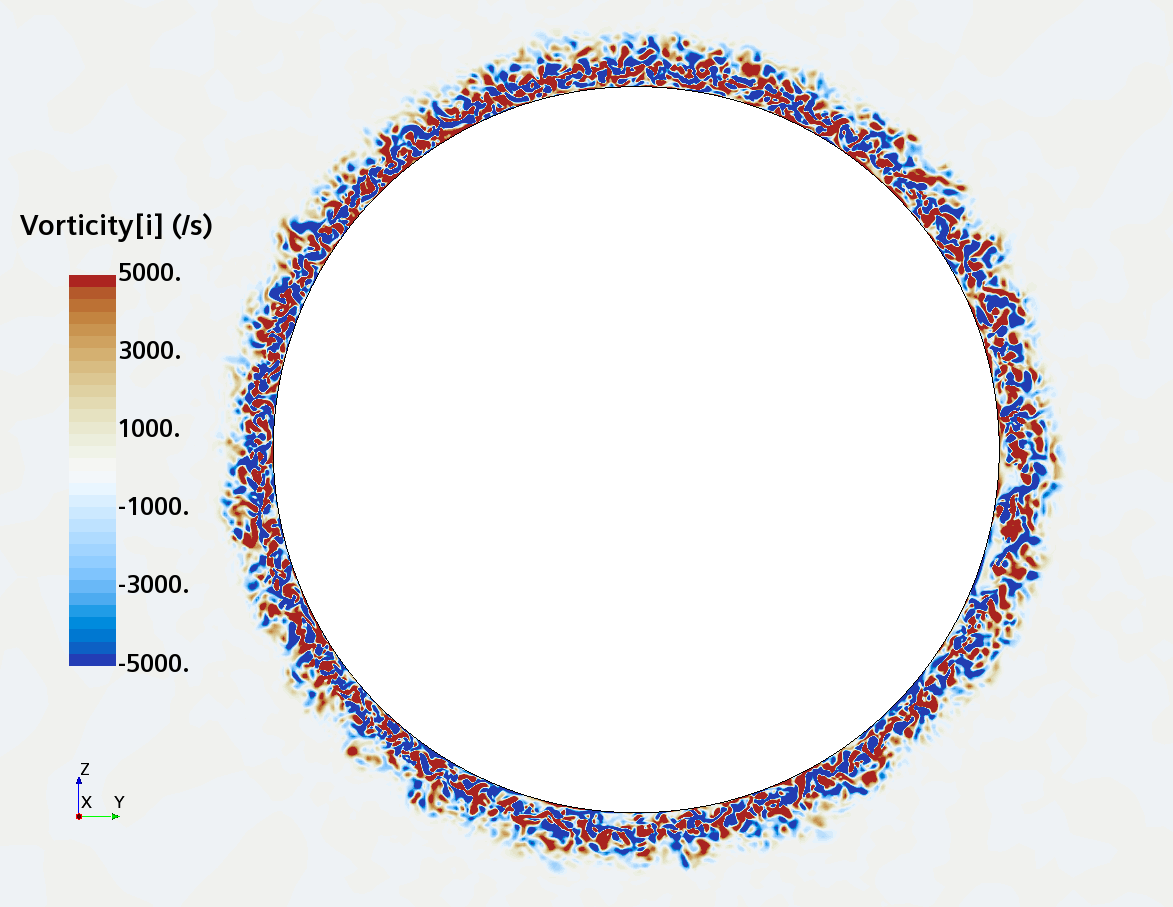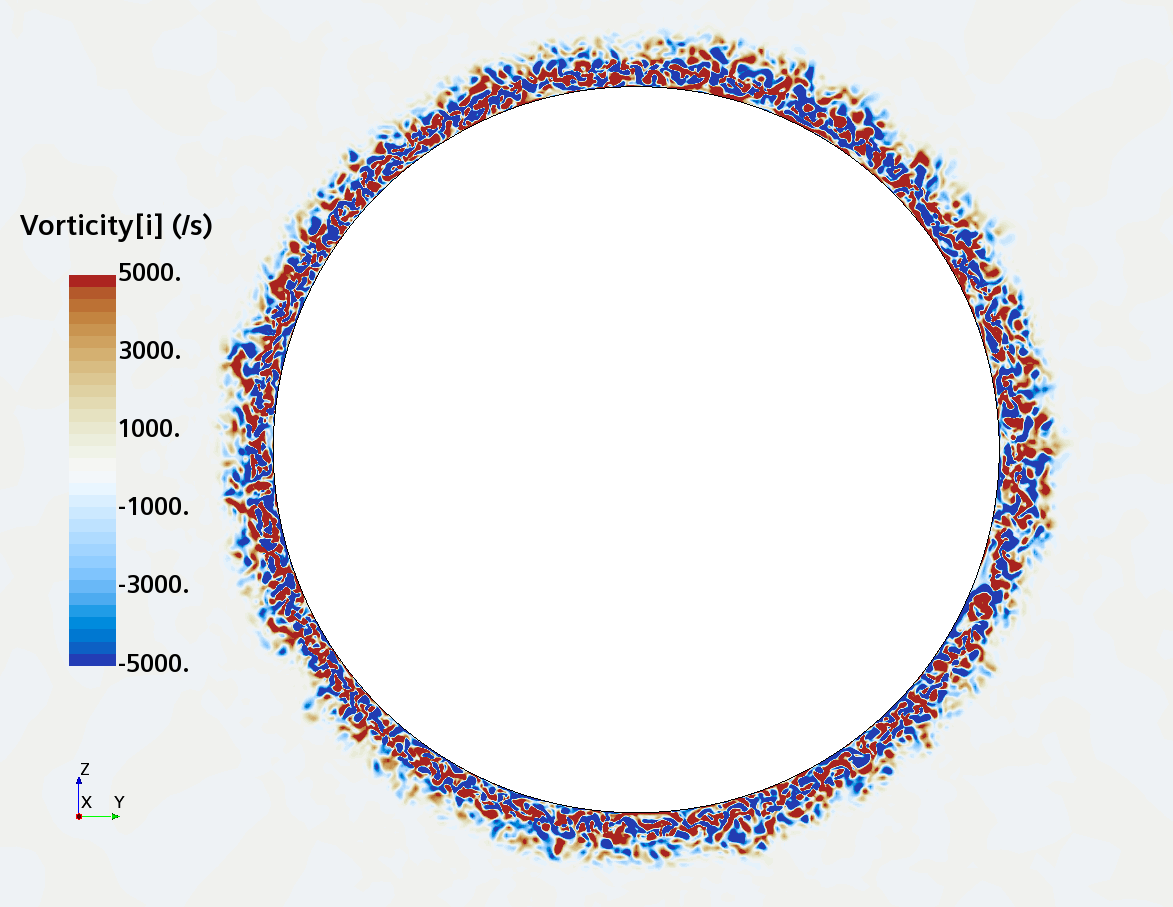
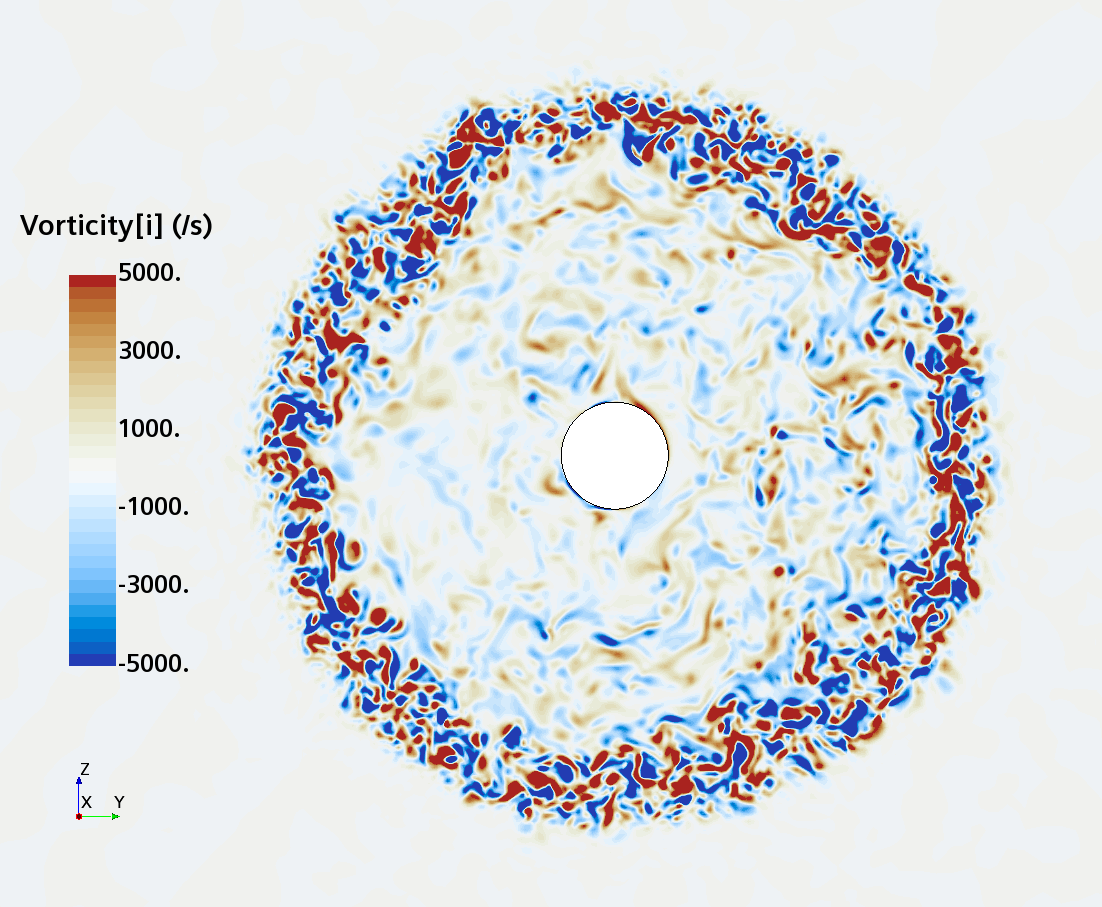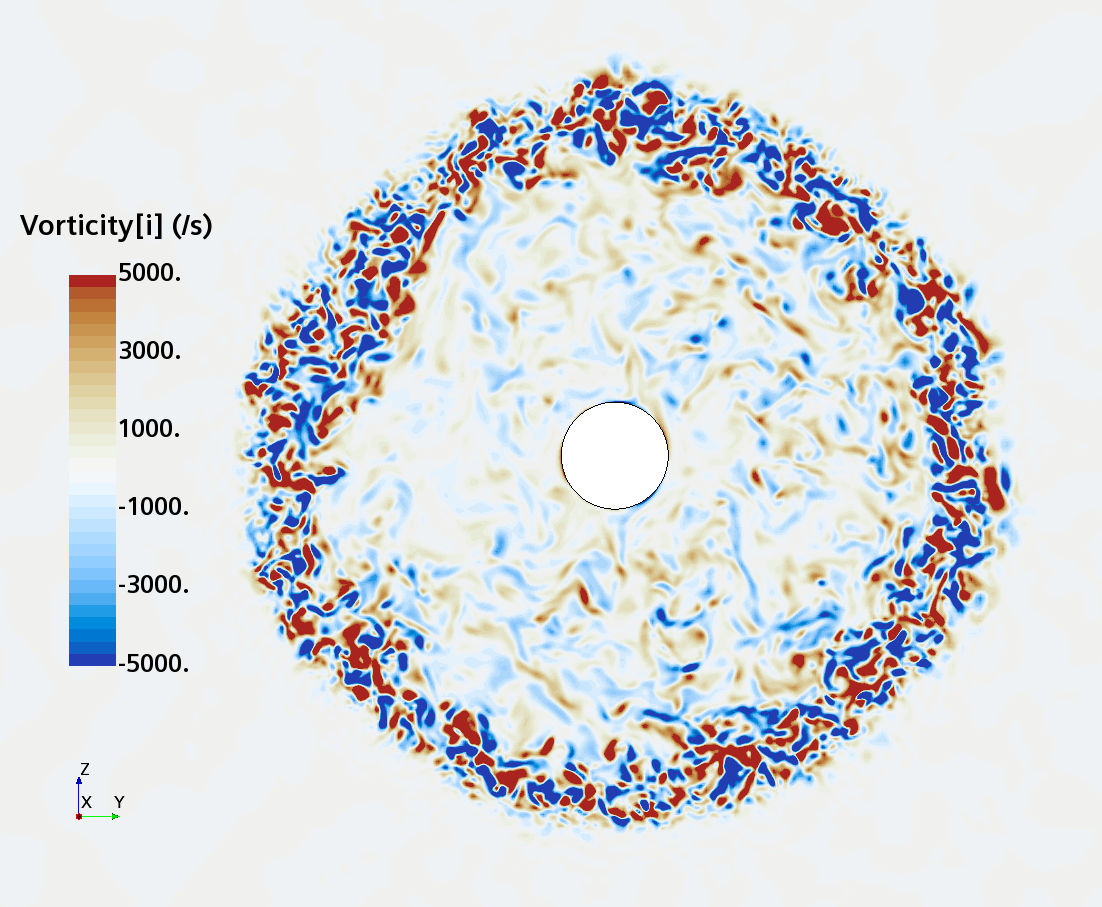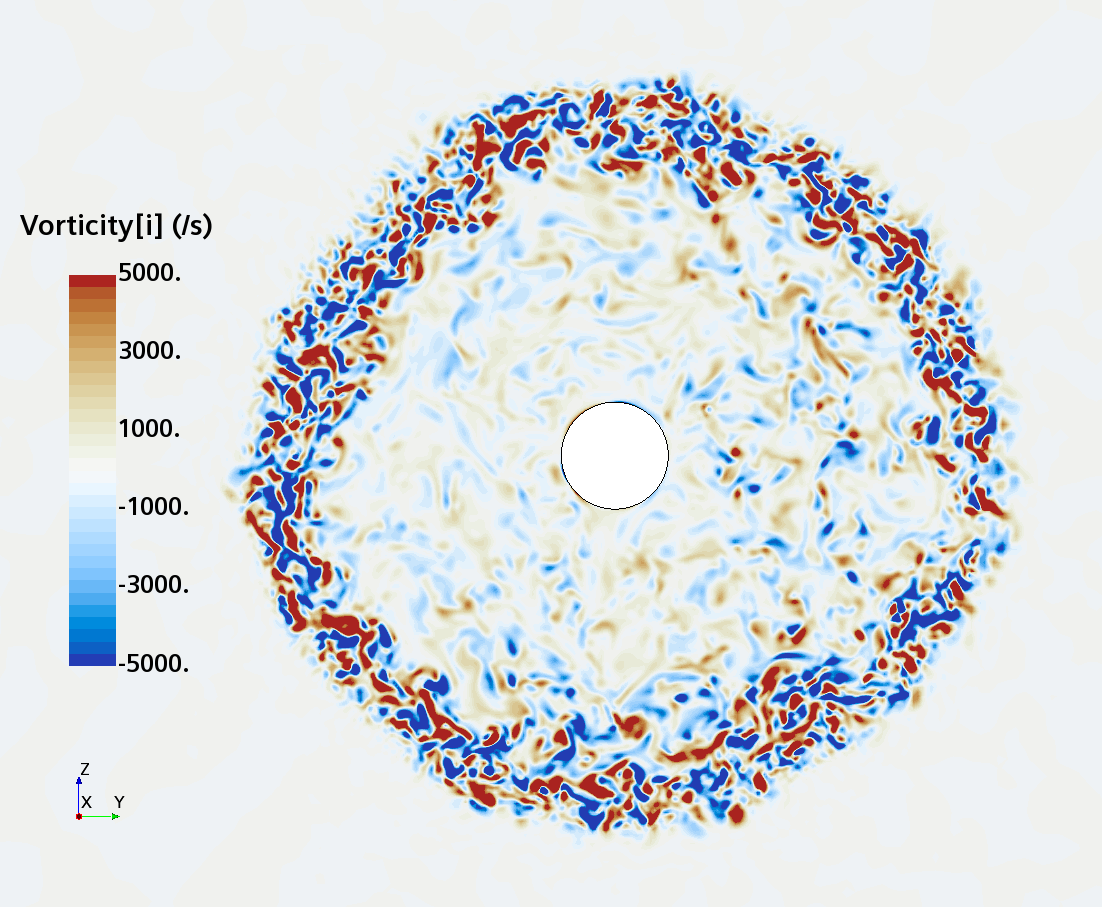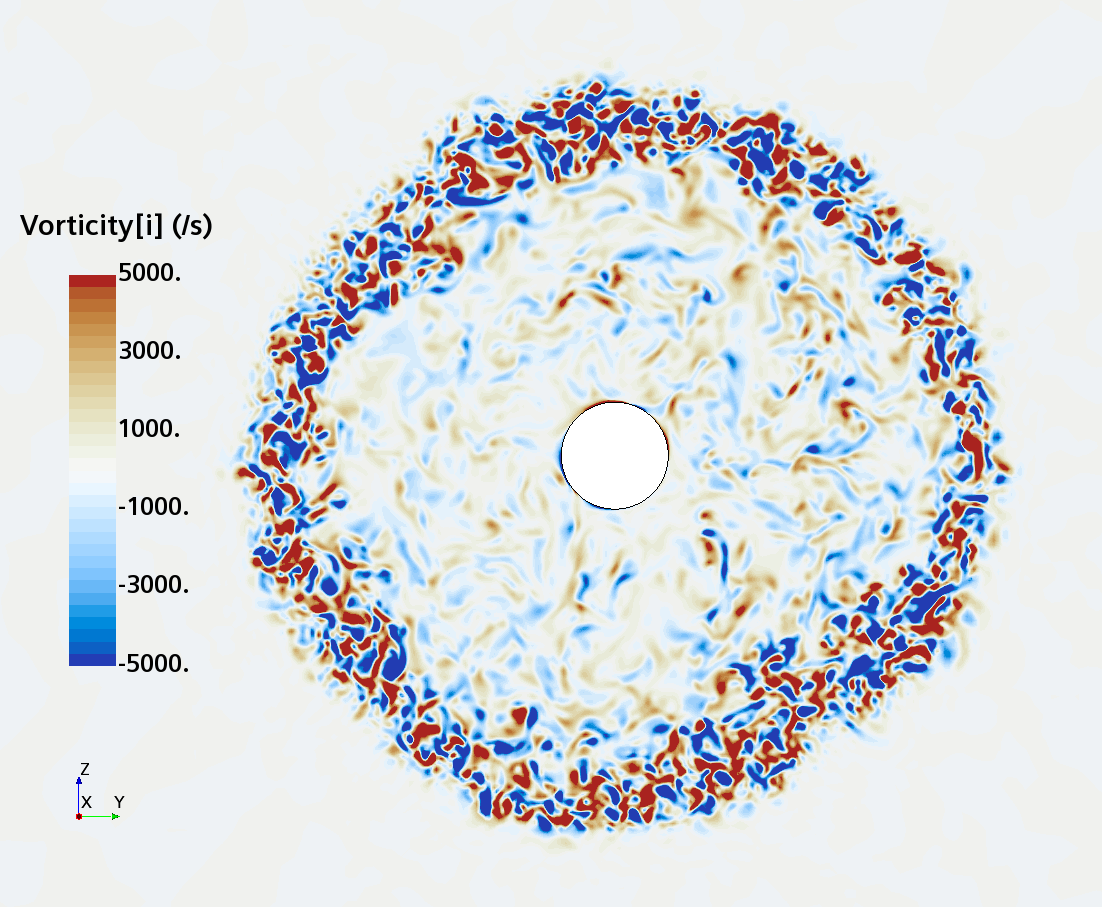
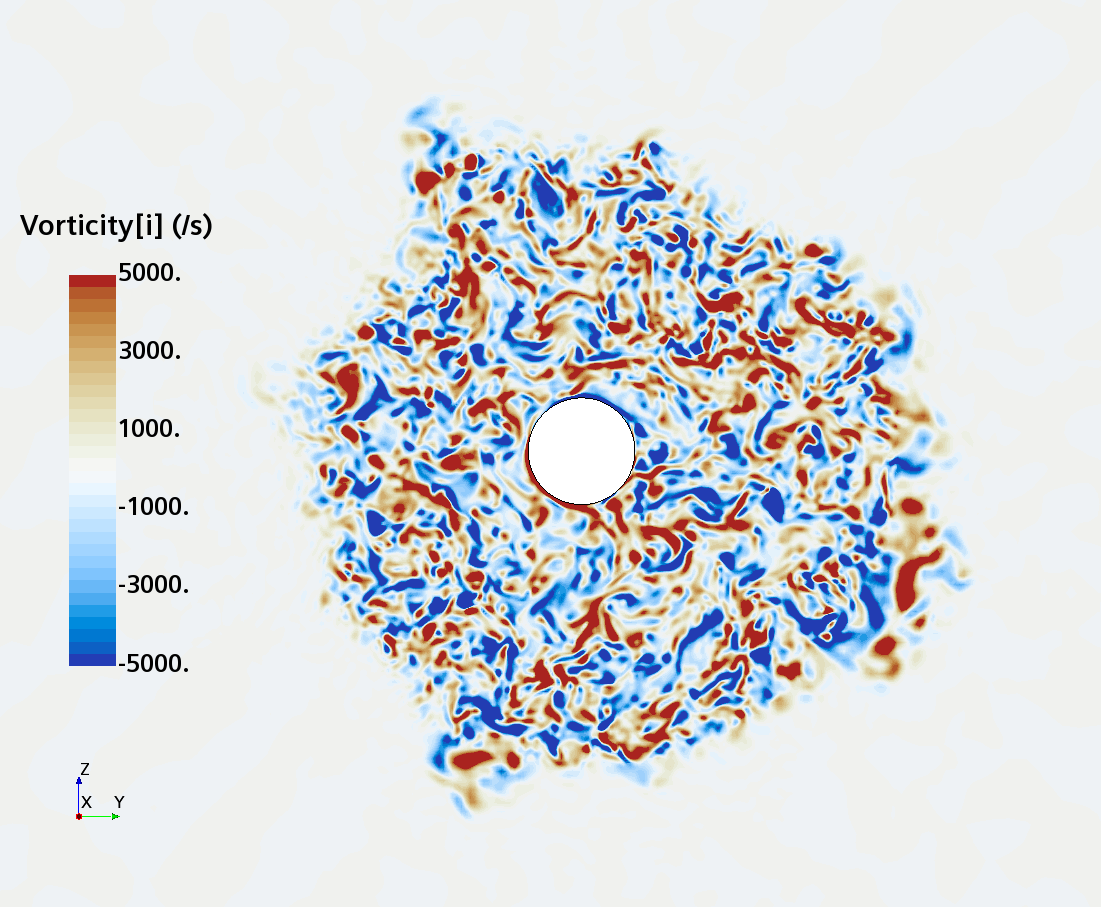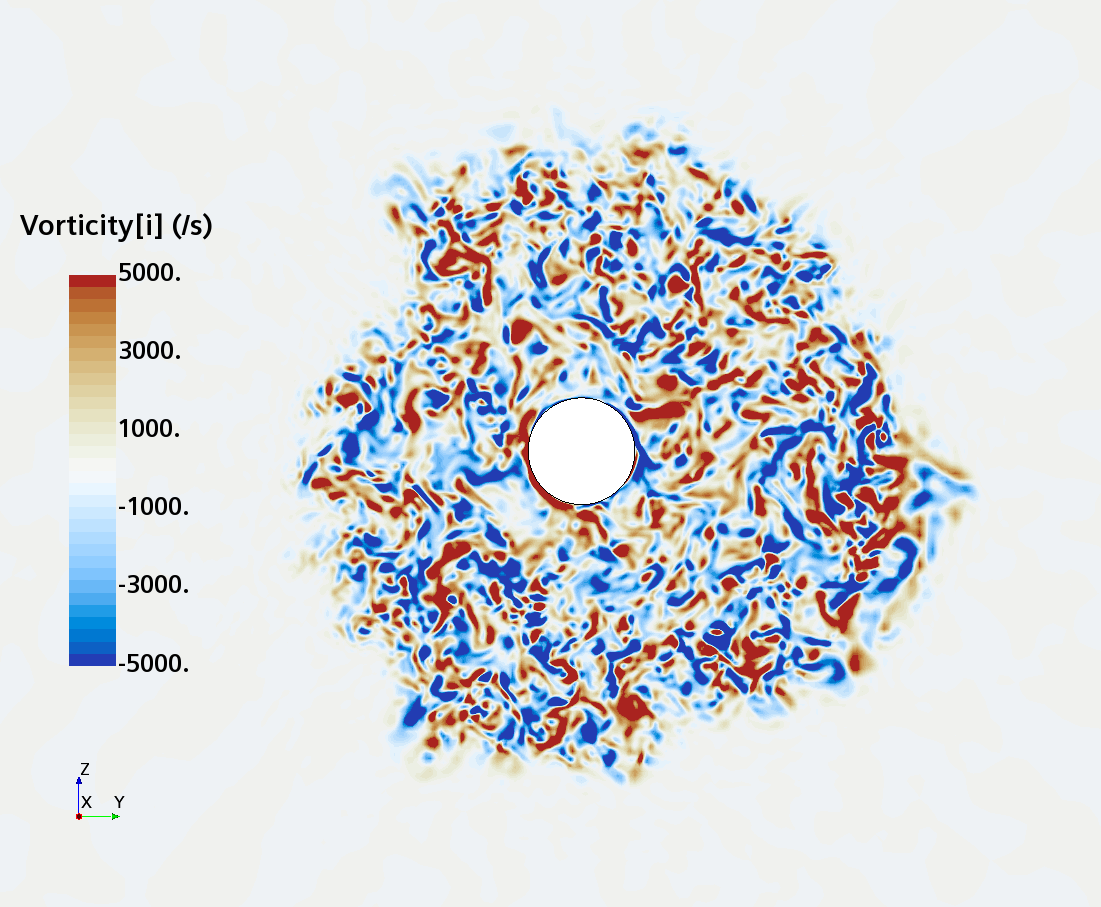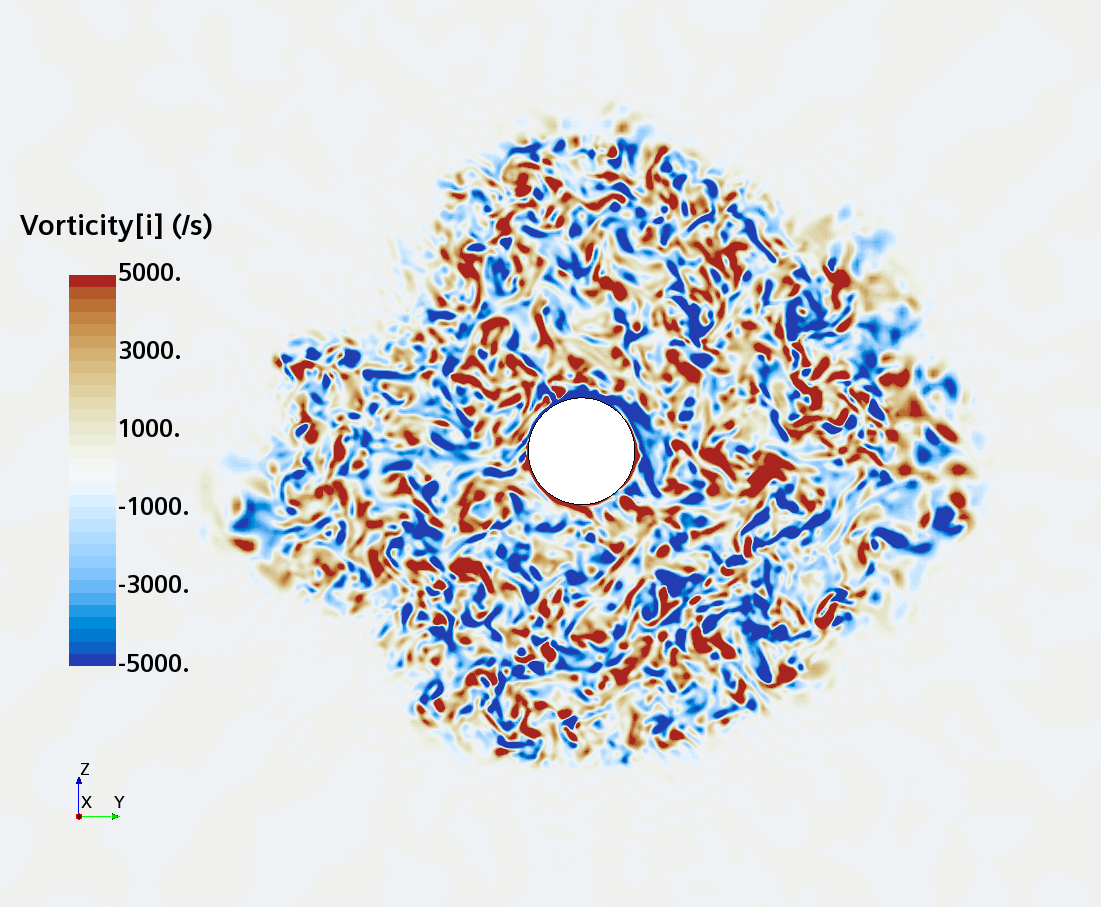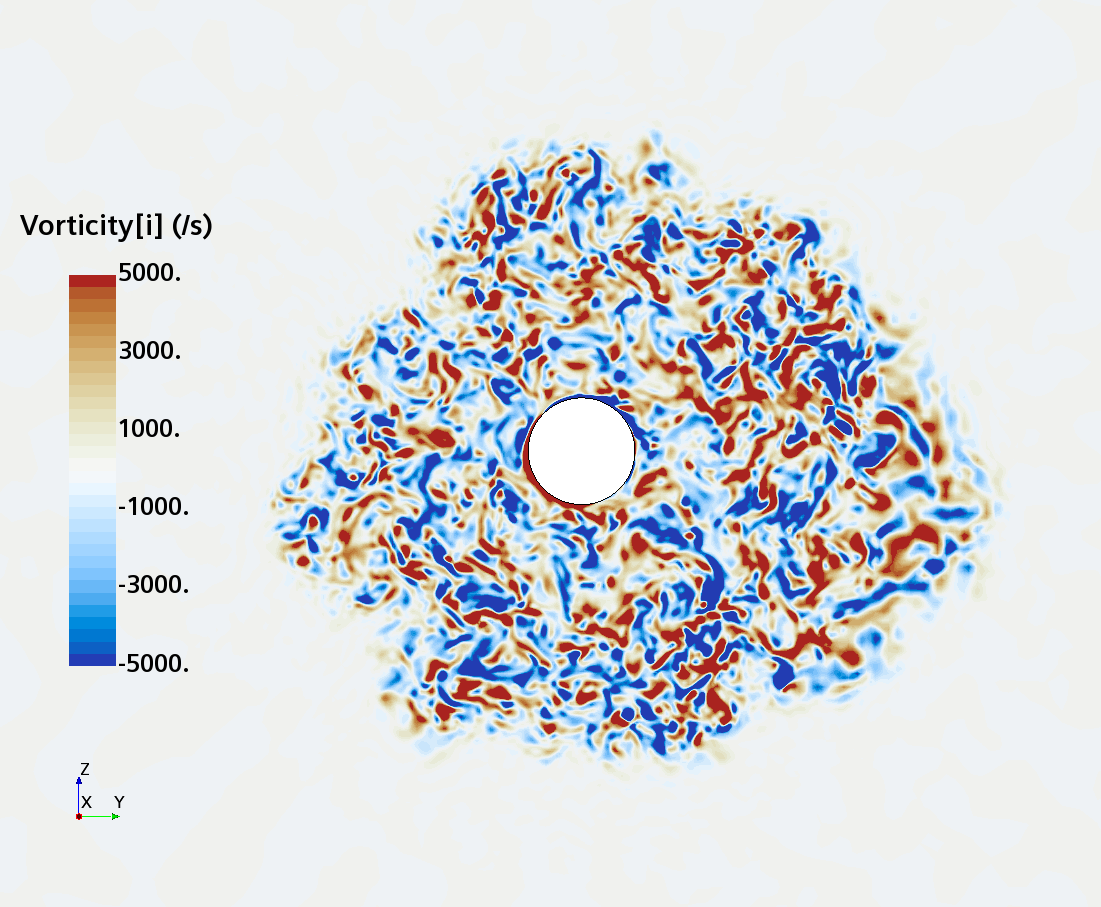
Instantaneous pattern of turbulent flow around a sphere held by a rear stick at Re = 50,000 (LES): animation of vorticity variation for a sphere with a trip wire in cross-section at 1/4 of diameter, 1/2 diameter, and 1 diameter downstream of sphere center, respectively, from top to bottom. The top two animations show a higher intensity of turbulence at the outer edge of the separation zone (highest shear) and lower intensity within separation zone. One diameter downstream of sphere center the whole wake is strongly turbulent and already beginning to meander around the stick (the flow separation zone is much shorter than for the smooth sphere). See Section 10.3.4.2 in the book for more details.

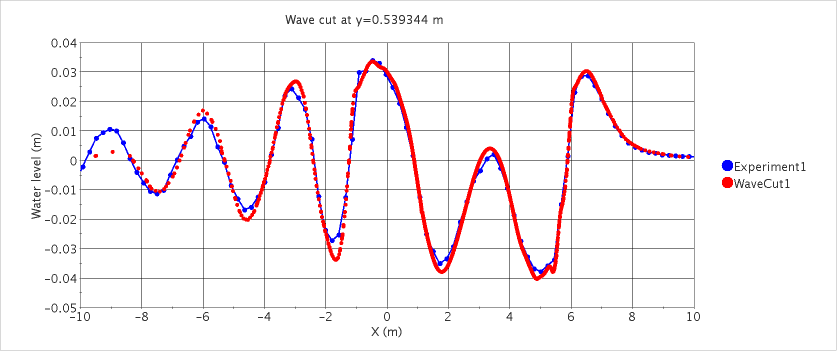
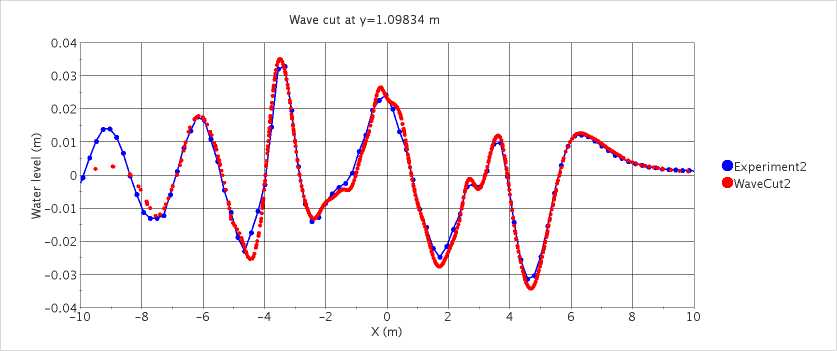
Free-surface flow around a container ship (model scale, fixed): wave pattern (upper) and comparison of predicted and measured wave profiles along two lines parallel to hull (middle and lower). See Section 13.10.1 for examples of flow around floating bodies.

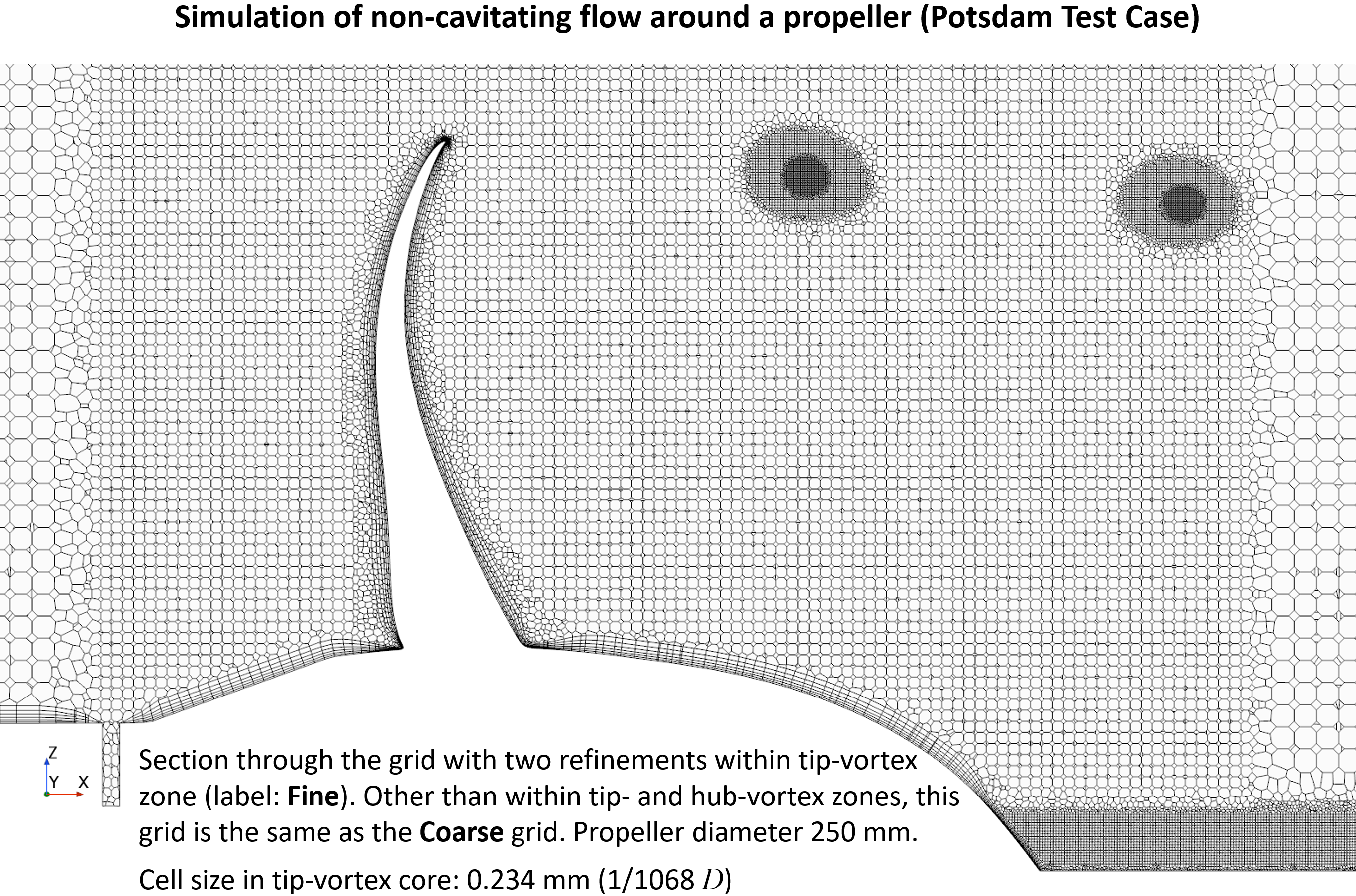
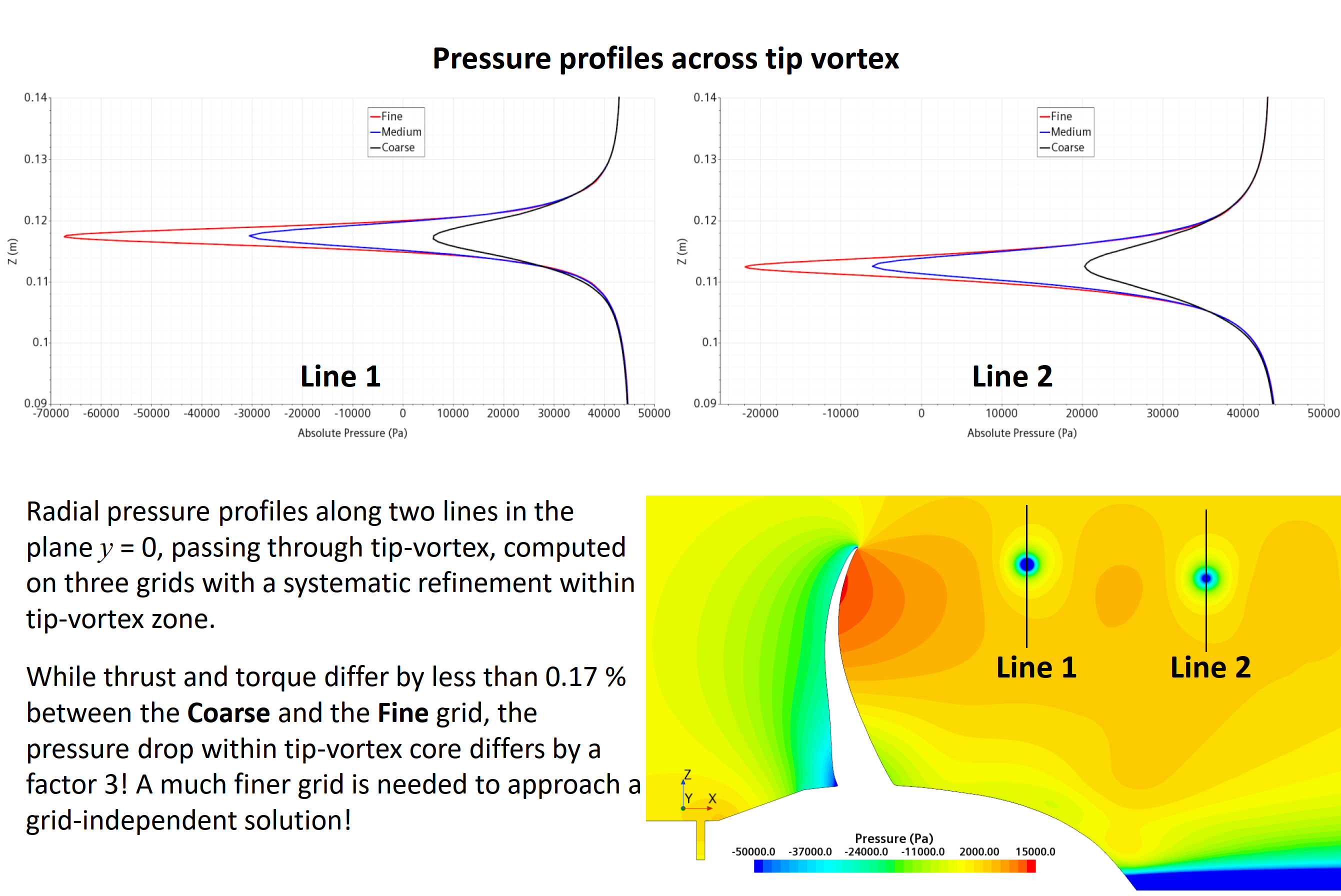
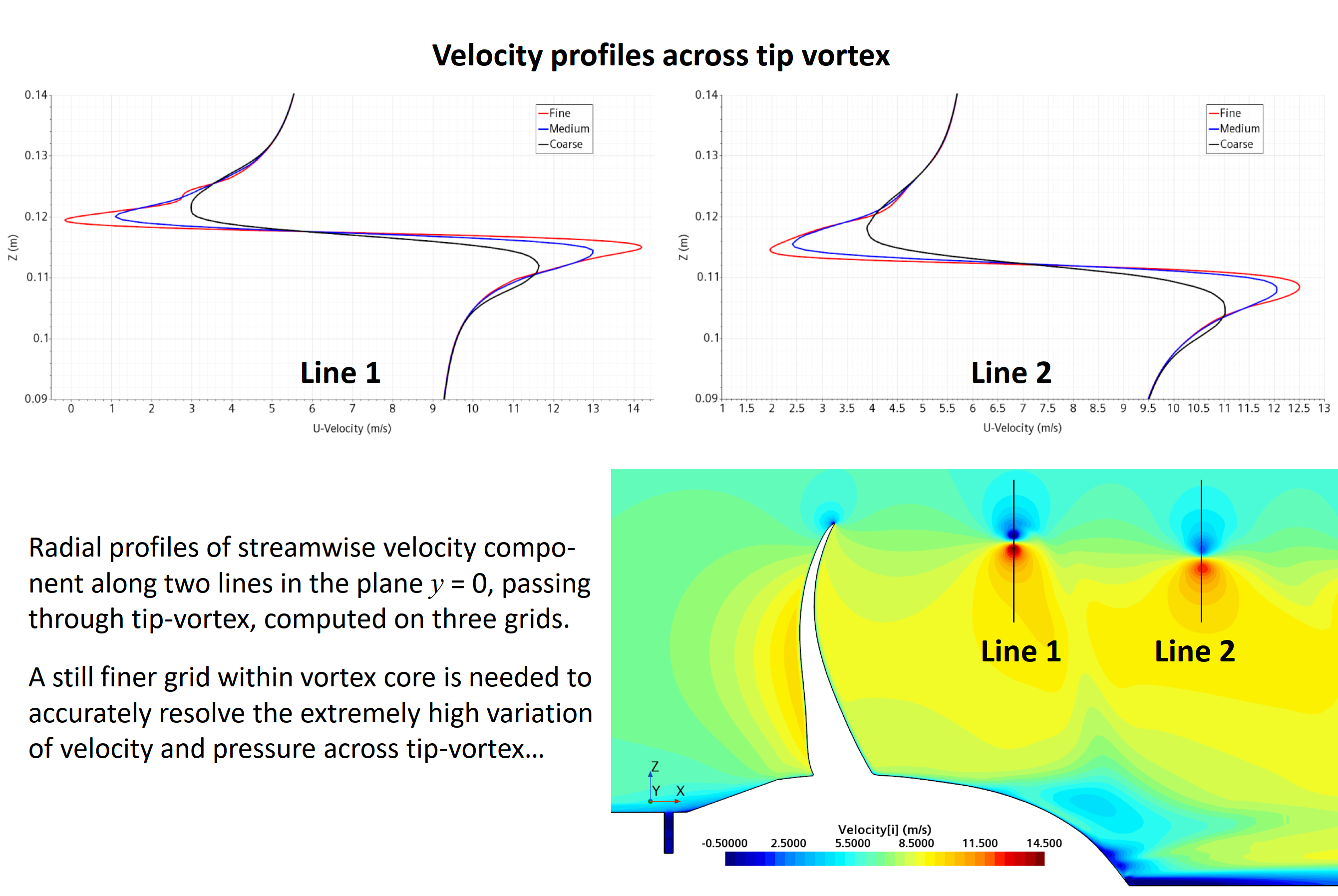
Simulation of flow around a propeller in a uniform flow (open-water test), with pronounced tip vortexes: local grid refinement within tip-vortex zone (top) and pressure (middle) and velocity (bottom) profiles across tip vortex. Both velocity and pressure very extremely rapidly across tip vortex, which requires extremely fine grid to accurately predict extrema in velocity and pressure profiles, which is essential in order to accurately predict tip-vortex cavitation (see Section 13.8 in the book).

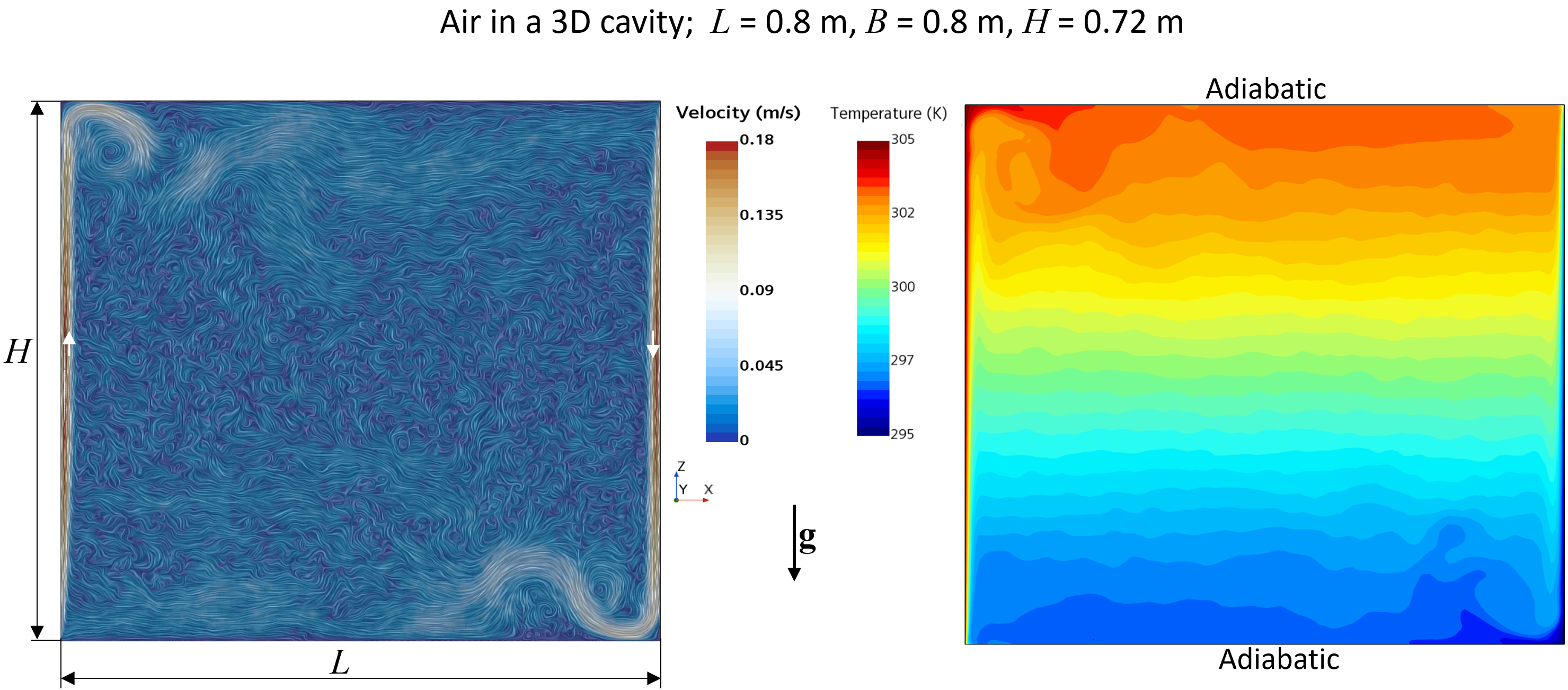
Instantaneous pattern of a turbulent, buoyancy-driven flow in the symmetry plane of a cubic cavity at a high Rayleigh-number (left) and the corresponding temperature field (right). White arrows indicate flow direction along isothermal vertical walls. Note stable stratification with nearly horizontal isotherms in the central part of the cavity.

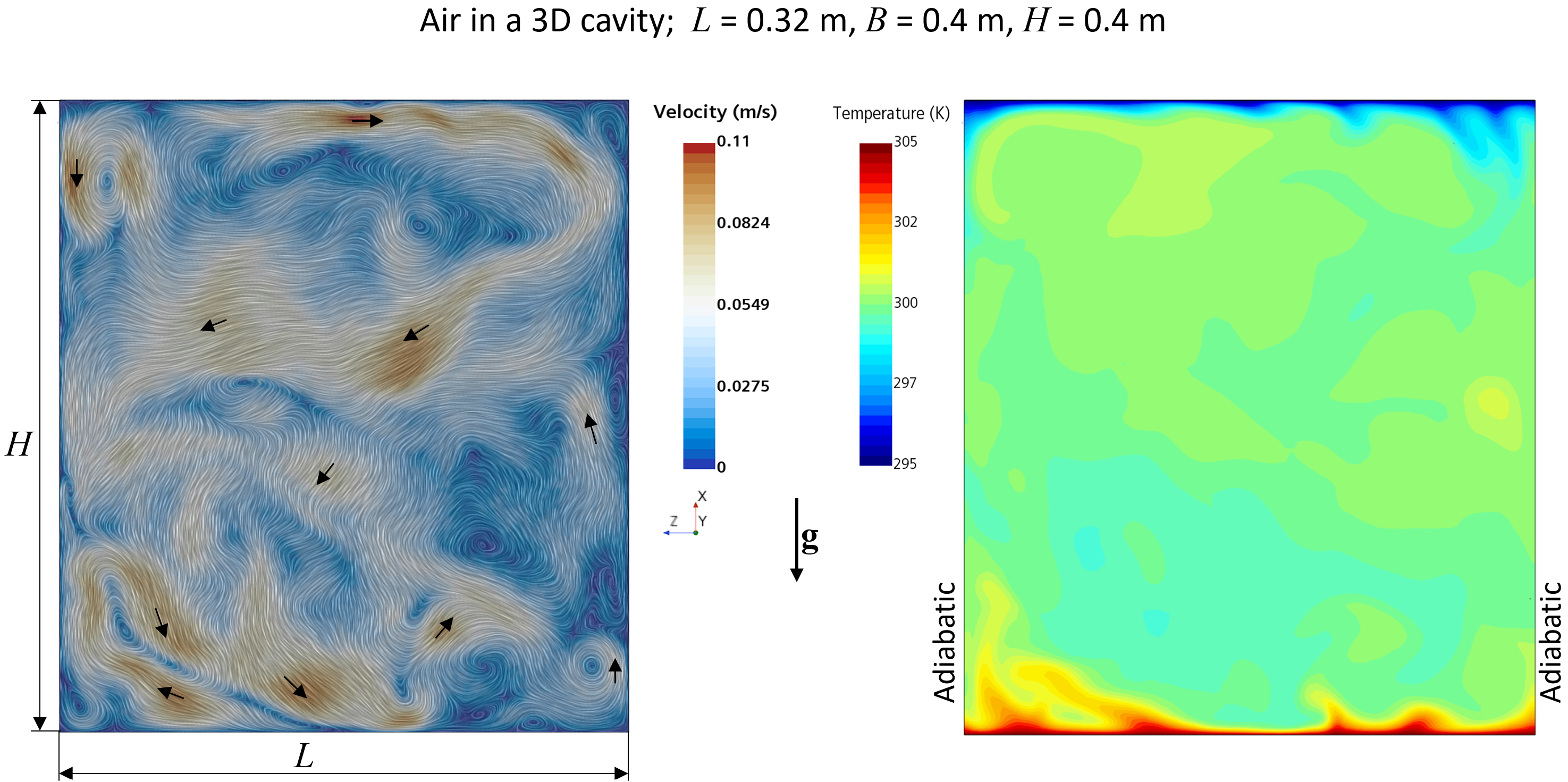
Instantaneous pattern of a turbulent, buoyancy-driven flow in the symmetry plane of a cubic cavity at a moderate Rayleigh-number (left) and the corresponding temperature field (right). This is the case of unstable stratification (hot wall at the bottom, cold wall at the top). Black arrows indicate the flow direction in the section plane. Note that the flow is three-dimensional; fluid flows also in the direction normal to the section plane.

Downloads

Here some sample codes are made available; the current offering is listed below and more is to come in future. Download compressed directories and read Readme-files in them for further details.

Sample codes for testing the order of various approximations (interpolation to compute variable values at face centers; approximations of surface integrals by midpoint and Simpson's rule), used to generate results presented in Sect. 4.7.1. Click here to download.

Sample codes for solving one-dimensional convection-diffusion problems, used to obtain results presented in Sect. 3.10 and 6.4. Click here to download.

Sample codes for solving two-dimensional and three-dimensional Laplace-equation using a variety of linear equation solvers (including multigrid versions of Gauss-Seidel, ILU and ICCG solvers). Click here to download.

Sample codes for solving two-dimensional steady and unsteady convection-diffusion problems (Laplace-equation, Poisson-equation and scalar transport in a given velocity field), used to obtain results presented in Sect. 6.4. Click here to download.

Sample codes for solving two-dimensional Navier-Stokes equations on a Cartesian grid using staggered variable arrangement. Click here to download.

Sample codes for solving two-dimensional Navier-Stokes equations on a Cartesian grid using colocated variable arrangement, set up for lid-driven and buoyancy-driven cavity flows. Click here to download.

Sample codes for solving two-dimensional Navier-Stokes equations on a Cartesian grid using colocated variable arrangement, set up for pipe and channel flows. Click here to download.

Sample codes for solving thre-dimensional Navier-Stokes equations on a Cartesian grid using colocated variable arrangement and multigrid acceleration of SIMPLE-iterations, set up for lid-driven and buoyancy-driven cavity flows. Click here to download.

Sample codes for solving two-dimensional Navier-Stokes equations (laminar flow) on body-fited structured non-orthogonal grids using colocated variable arrangement, including several examples. Click here to download.

Sample codes for solving two-dimensional Navier-Stokes equations (laminar flow) on body-fited structured non-orthogonal grids using colocated variable arrangement, including moving grids and boundary conditions with specified pressure. Click here to download.

Sample codes for solving two-dimensional Reynolds-averaged Navier-Stokes equations (turbulent flow at high Reynolds-number, using wall functions) on body-fited structured non-orthogonal grids using colocated variable arrangement, including several examples. Click here to download.